Число n є дільником числа m, якщо число m ділиться на число n без остачі.
Дільники числа 18: 1, 2, 3, 6, 9, 18.
Дільники числа 24: 1, 2, 3, 4, 6, 12, 24.
Найбільший спільний дільник чисел 18 та 24 - це 6. Скорочено: НСД (18, 24) = 6.
НСД (m, n) - це найбільше з чисел, на яке діляться і m, і n.
Два числа m та n називаються взаємно простими, якщо їх НСД (m, n)=1. Наприклад, НСД(9, 16)=1. Не плутати з простими числами! Числа 9 та 16 не прості, бо мають дільники окрім 1 та самого числа.
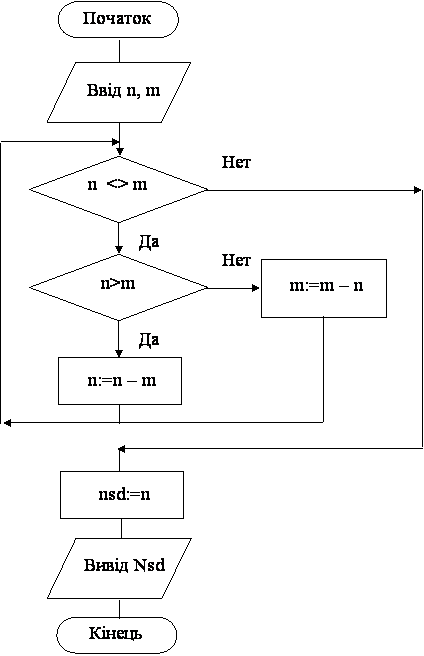
Алгоритм Евкліда дозволяє знайти НСД двох натуральних чисел.
Суть алгоритму Евкліда – два числа порівнюють і від більшого віднімають менше до тих пір, поки числа не стануть рівними. Число, якому вони стануть рівними, і є їх найбільший спільний дільник.
Алгоритм Евкліда змінює вхідні дані! Тому рекомендується їх запам’ятовувати у інші змінні.
Знайдіть НСД(n, m) найбільший спільний дільник двох натуральних чисел за алгоритмом Евкліда.
| Ввід | Вивід |
|---|---|
| 18 24 | 6 |
| 9 16 | 1 |
Вхідні:
n – перше натуральне число (цілого типу)
m – друге натуральне число (цілого типу )
Вихідні:
nsd – найбільший спільний дільник чисел n та m (цілого типу)

|
var n,m,nsd:word; begin read(n,m); while n<>m do if n>m then n:=n-m else m:=m-n; nsd:=n; writeln(nsd); end. |
Проводячи трасування програми, потрібно обов’язково дивитись текст програми!
| Оператор | n | m | nnsd | Пояснення |
|---|---|---|---|---|
| read(n,m) | 18 | 24 | Введення чисел | |
| while n<>m do | Заголовок циклу. Перевірка умови. Умова вірна, тому перехід на початок циклу. | |||
| if n>m then | Перевірка умови. Умова невірна, тому виконується оператор, що стоїть після else. | |||
| m:=m-n | 6 | Зміна числа m | ||
| while n<>m do | Заголовок циклу. Перевірка умови. Умова вірна, тому перехід на початок циклу. | |||
| if n>m then | Перевірка умови. Умова вірна, тому виконується оператор, що стоїть після then. | |||
| n:=n-m | 12 | Зміна числа n | ||
| while n<>m do | Заголовок циклу. Перевірка умови. Умова вірна, тому перехід на початок циклу. | |||
| if n>m then | Перевірка умови. Умова вірна, тому виконується оператор, що стоїть після then. | |||
| n:=n-m | 6 | Зміна числа n | ||
| while n<>m do | Заголовок циклу. Перевірка умови. Умова невірна, цикл завершується. Перехід на оператор після циклу | |||
| nsd:=n | 6 | Запам’ятовуємо значення НСД у змінній nsd | ||
| writeln(nsd) | Вивід значення НСД на екран. |
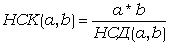 .
.
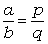 .
Пояснення: за алгоритмом Евкліда знаходимо НСД(a, b) та ділимо чисельник та знаменник на це число.
.
Пояснення: за алгоритмом Евкліда знаходимо НСД(a, b) та ділимо чисельник та знаменник на це число.
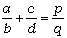 . Пояснення: скласти два дроби. Чисельник дорівнює
a*d+b*c. Знаменник дорівнює b*d. Потім за алгоритмом Евкліда знаходимо НСД
чисельника та знаменника і ділимо чисельник та знаменник на це число.
. Пояснення: скласти два дроби. Чисельник дорівнює
a*d+b*c. Знаменник дорівнює b*d. Потім за алгоритмом Евкліда знаходимо НСД
чисельника та знаменника і ділимо чисельник та знаменник на це число.