 |
|
П.Я. Пасіхов - |
|
|
П.Я. Пасіхов - |
Єдиність границі. Обмеженість збіжної послідовності
Якщо вказано правило, за яким кожному натуральному числу n відповідає певне число xn, то кажуть, що задана послідовність
x1, x2, …, xn, … = {xn}. (1)
Числа x1, x2, … називаються членами послідовності. Енний член xn, з якого можна отримати будь-який член послідовності при n = 1, 2, 3, … , називається загальним членом.
Отже, послідовність– це функція, задана на множині натуральних чисел.
Приклади послідовностей:
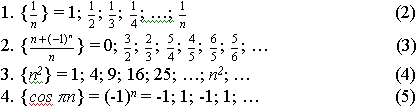
(5) показує, що члени послідовності можуть бути однаковими.
Якщо із послідовності (1) виділити нескінченну множиу членів, зберігаючи порядок їх слідування, то отримаємо деяку послідовність
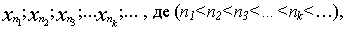
яку називають підпослідовністю даної послідовності.
Приклад. Послідовності -1; -1; -1; … та 1; 1; 1; … є підпослідовностями послідовності (5).
Означення. Послідовність {xn} називається обмеженою, якщо існує число k ≥ 0, що для всіх n виконується нерівність ׀xn׀ ≤ k.
Зобразимо елементи послідовності (2) та (3) на числовій прямій.
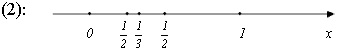
Точки наближаються до нуля.
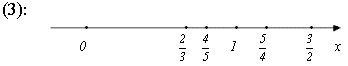
Точки наближаються до одиниці.
Видно, що члени послідовності (2) скупчуються біля нуля справа, а члени послідовності (3) скупчуються біля одиниці з обох сторін.
Спільна властивість цих послідовностей
в тому, що віддалі
|
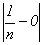
та |
|
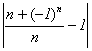
можуть стати як завгодно малими. У цих випадках число 0 та число 1 називають границями послідовностей (2) та (3) відповідно.
Абстрагуючись від цих конкретних прикладів, природньо приходимо до поняття границі послідовності .
Означення. Число a називають границею послідовності x1, x2, …, xn, …, якщо для довільного ε>0 знайдеться номер no такий, що нерівність
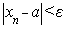(6)
 |
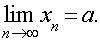Зауваження:
1) Якщо в послідовності всі числа однакові (сталі), то |xn-a|=|a-a|=|0|=0<ε.
Висновок: границя сталої ε сама стала.
2) Модуль в означенні використано для того, щоб охопити всі можливі випадки прямування xn до границі a. Для нас байдуже, чи це прямування здійснюється справа (як у прикладі 2), чи з обох сторін (як у прикладі 3), чи зліва, а важливо лише те, про що говориться в означенні – віддаль між точками xn та числом a повинна прямувати до нуля, тобто ставати як завгодно малою.
3) Номер no – це значення номера n, після якого виконується нерівність (6) |xn-a|<ε, однак слід пам’ятати, що коли (6) виконується для деякого n>no, то ця ж нерівність буде виконуватись для кожного n1>n. Номер no залежить від ε і зі зменшенням ε зростає no.
Із заданням ε no визначається не однозначно. Саме тому означення не вимагає, щоб для заданого ε вказувати найменше із можливих значень no.
З геометричної точки зору a – границя послідовності чисел xn, якщо в довільному околі точки a містяться майже всі члени розглядуваної послідовності. Слово “майже” означає, що поза ε-околом точки a може бути хіба що скінченна множина членів послідовності.
4) Якщо послідовність (1) має своєю границею число а, то цю ж саму границю мають всі її підпослідовності. Це випливає з геометричого тлумачення.
Послідовність, яка має своєю границею певне число, називають збіжною до цього числа. У протилежному випадку послідовність називається розбіжною.
Приклад. Послідовність (5) розбігається (не має границі), так як її підпослідовності прямують до різних границь:
-1; -1; -1; … → -1,
1; 1; 1; … → 1.
Теорема. Якщо послідовність має граицю,
то тільки одну.
Доведення.
За умовою xn →
a.
Розглянемо число b ≠
a. Задамо ε-окіл точки а, де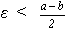 
.
За означенням границі поза ε-околом точки
а міститься скінченна множина
точок, а це означає, що ε-окіл
точки b не містить нескінченної множини
членів послідовності. Отже, число b не може бути границею послідовності
xn.
Теорему доведено.
Теорема. Кожна збіжна послідовність обмежена.
Доведення.
З умови теореми випливає, що послідовність xn збіжна, тобто існує границя. Отже, для ε>1 знайдеться таке no, що для довільного n>no
|xn-a|<1.
Тому |xn| = |(xn-a)+а| ≤ |xn-a|+|a| < |a|+1.
Візьмемо найбільше з чисел
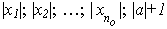
і
позначимо через
k.
Тоді для довільного n маємо: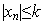 
,
а це означає обмеженість розглядуваної
послідовності.
Теорему доведено.