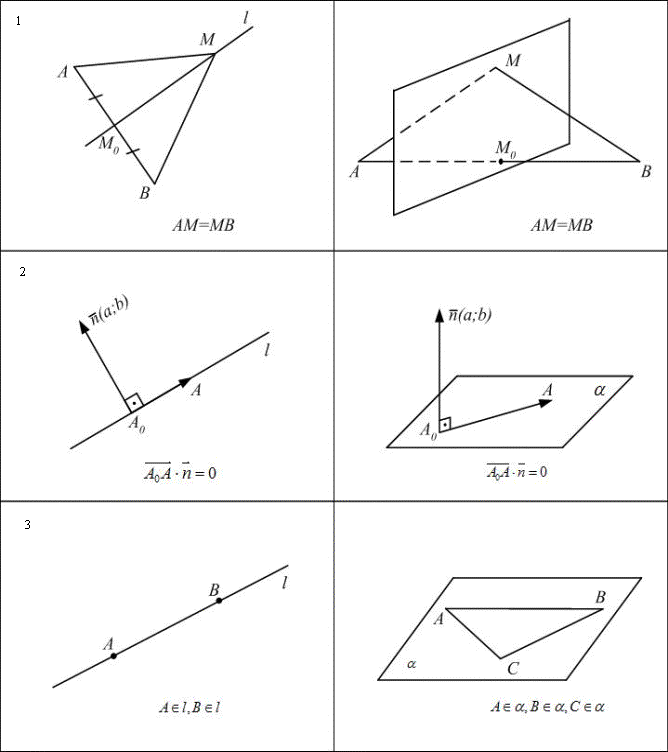
Як відомо, аналогом прямої на площині є площина у просторі. Тому не дивно, що рівняння прямої та відповідне рівняння площини - одного типу ( лінійне рівняння, відповідно з двома і трьома змінними). Було б зручно, щоб і виводились вони схожими методами. Однак, рівняння прямої в планіметрії ми виводимо, користуючись властивістю середнього перпендикуляра, а рівняння площини – “за допомогою” вектора нормалі. Це й зрозуміло, адже в планіметрії вектори вивчаються значно пізніше, а в стереометрії навпаки – вектори розглядаються раніше ніж рівняння площини.
Було б недоцільно, щоб знання учнів відтворювали, вимушені обставинами методичного характеру, прогалини в навчальному матеріалі. Тим більше, що у допитливих учнів природно виникає питання: чи можна рівняння прямої одержати за допомогою векторів, а рівняння площини – не використовуючи їх?
Досвід переконує, що розділ “Декартові координати і вектори у просторі” корисно завершувати системним оглядом матеріалу. Для цього, зокрема, можна використовувати таблицю “Рівняння фігур”, наведену далі, та записи відповідних виведень, які виконуються так, щоб ілюструвати їх аналогічність.
У таблиці схематично представлені три методи виведення рівняння площини та відповідного рівняння прямої, а саме:
1.
метод геометричних місць;
2.
з застосуванням скалярного
добутку векторів;
3.
з використанням точок, що
визначають площину (пряму).

|
Геометричним місцем точок, рівновіддалених від кінців відрізка є пряма l,що проходить через середину цього відрізка перпендикулярно до нього. Нехай кінці відрізка –
|
Геометричним місцем точок, рівновіддалених від кінців відрізка є площина α, що проходить через середину цього відрізка перпендикулярно до нього. Нехай кінці відрізка -
|
тоді
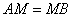
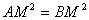
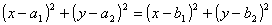 |
|
Спрощуючи, одержимо
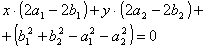 |
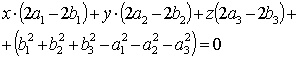
|
Позначивши
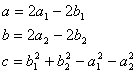
|
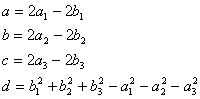
|
Маємо
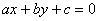
|
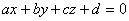
|
2. Оскільки учні ознайомлені із застосуванням скалярного добутку до виведення рівняння площини, можна запропонувати у якості домашньої роботи виведення відповідного рівняння прямої.
3.
Рівняння прямої, що проходить через 2
задані точки, як і рівняння площини, що
проходить через три задані точки, доцільно
виводити для
конкретно заданих точок.
Знайдемо рівняння
площини, що проходить точки
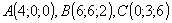
|
Знайдемо рівняння прямої,
що проходить через
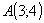 та
та
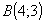
|
Загальне рівняння
|
прямої |
площини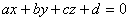 оскільки точки A,B і C належать шуканій площині, то їх координати перетворюють рівняння площини у істину рівність |
Маємо
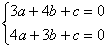
|
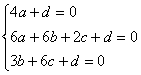
|
Звідси
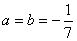
|
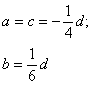
|
Підставивши значення
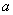 і
і
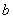 через
через
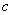
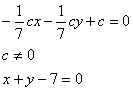
|
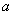 ,
,
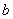 і
і
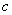 через
через
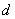
|
Знання, стаючи системними, стають і продуктивними.