7.1.
а) (x+y)/(x-1/2)-(x-z)/(x*y); б) (1+z)*(x+y/z)/(a-1/(1+x*x)); в) x**(n*(m+2)) + x**(n**m); г) (a+b)**n/(1+a/(a**m-b**(m-n))); д) (a[i]**(2*l) + b[j+1]**(2*k)) * (3**n-x*x*y)/(z-(d[i,j+1]+1)/(z+ y/sqrt(t*t+x*y*z))); е) sqrt(abs(sin(x)**2))/(3.01*x - exp(2*x)); ж) abs(cos(x**3) - sin(y)**2) / (abs(ln(x))**(1/4) + x*y); з) ln(y**(-sqrt(abs(x+1)))) * sin(arctg(z))**2; и) r[i,j]**abs(x-y) - 0.15*abs(sin(exp(-z**8))); к) a**((x+y)/2) - ((x-1)/(abs(y)+1))**(1/3)*exp(-(y+u/2)).
7.2.
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() ;
д)
;
д) ![]() ;
е)
;
е) ![]() ;
ж)
;
ж) ![]() ;
з)
;
з) ![]() ;
и)
;
и) ![]() ;
к)
;
к) ![]() ;
л)
;
л) ![]() ;
м)
;
м) ![]() ;
н)
;
н) ![]() ;
о)
;
о) ![]() ;
п)
;
п) ![]() ;
р)
;
р) ![]() ;
с)
;
с) ![]() ;
т)
;
т) ![]() ;
у)
;
у) ![]() ;
ф)
;
ф) ![]() .
.
7.3. б) 16; в) 5,5; г) -256; д) 3; е) -2; ж) 1.8.
7.4. б) среднее арифметическое: (a+b+c+d)/4; среднее геометрическое: (a*b*c*d)**(1/4); в) sqrt(x*x+y*y); г) sin(x*3.14/180); д) 6*a*a; е) sqrt(3)*a/2; ж) абсцисса: (c1*b2-c2*b1)/(b1*a2-b2*a1); ордината: (c2*a1-c1*a2)/(b1*a2-b2*a1).
7.5. б) нет; в) да; г) да; д) да; е) нет;
7.6.
б) (x < a) или (x > b); в) ((x>=a) и (x<=b)) или ((x>=c) и (x<=d)); г) ((x < a) или (x > b)) и ((x < c) или (x > d)); д) mod(k,2)=1; е) (mod(k,5)=0) и (k > 99) и (k < 1000); ж) (mod(i,2)=1) и (mod(j,2)=0); з) a1*b2=a2*b1; и) (c < a) и (b > a); к) (a=-b) или (a=-c) или (a=-d) или (b=-c) или (b=-d) или (c=-d); л) ((mod(a,2)=0) и (mod(b,2)=0)) или ((mod(a,2)=0) и (mod(c,2)=0)) или ((mod(b,2)=0) и (mod(с,2)=0)); м) (a>0) и (b>0) и (c>0) и (a+b>c) и (a+c>b) и (b+c>a); н) ((a1*b2=a2*b1) и (a1*c2=a2*c1)) или ((a1*c2=a2*b1) и (a1*b2=a2*c1)) или ((a1*c2=b2*b1) и (a1*a2=b2*c1)) или ((a1*a2=b2*b1) и (a1*c2=b2*c1)) или ((a1*a2=c2*b1) и (a1*b2=c2*c1)) или ((a1*b2=c2*b1) и (a1*a2=c2*c1)); о) (y>5-5*x) и (y<5-x) и (y>0); п) (y<5-5*x)) или (y>5-x) или (y<0); р) (a=b) и (c=d) и (b=c).
7.7.
б)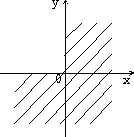 в)
в)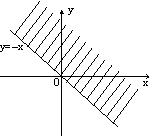 г)
г)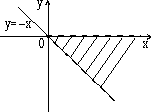 д)
д)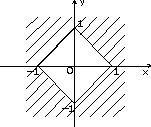 ж)
ж)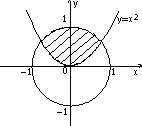 з)
з)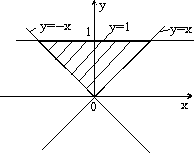 и)
и)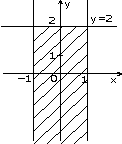 к)
к)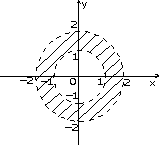
7.8.
а) (y>=1-x) и ((y<=0) или (x<=0)); б) (y<1) и (y>=x) и (y>=-x) (вариант ответа: (y<1) и (y>=abs(x))); в) (abs(x)<=1) и (abs(y)<1); г) ((x-1)*(x-1)+y*y<=4) и (y<=3-x) и (y>=x-3); д) (abs(x)<=3) и (abs(y)<=3) и (x*x+y*y>=9) и ((x>=0) или (y<=0)); е) (abs(x)+abs(y)<=2) и (sign(x)<>sign(y)) или (x*x+y*y<=4) и ((y>=2-x) или (y<=-x-2)); ж) ((y>=x*x) или (y<=-x*x)) и ((x>=y*y) или (x<=-y*y)); з) (((x+2)*(x+2)+y*y<=4) и ((x+2)*(x+2)+y*y>=1)) или (x>=-1); и) (((y<=0)=(y>=-x)) или ((x>=0)=(y>=x))) и (x*x+y*y<=1).
7.9. б) a=-19; b=-114; c=17; в) a=3; b=1,875; c=15; г) a=7; b=3; c=735; д) a=10; b=2; c=120; е) a=4; b=7; c=3; ж) a=16; b=100, c=11200.
7.10. б) c:=x[1]; x[1]:=x[2]; x[2]:=c; в) a[i]:=(a[i-1]+a[i+1])/2; a[i+1]:=0; a[i-1]:=a[i-1]+0.5; г) u:=max(max(x, y), z) + min(min(x-z,y+z), min(y,z)).
7.11.
а) если x <= -100 б) если x*x+y*y <= 1
то y:=sign(x)*abs(x)**(1/7) то z:=x*x+y*y
иначе если x < 100 иначе если y>=x
то y:=sign(x)*abs(x)**(1/3) то z:=x+y
иначе y:=sqrt(x) иначе z:=0.5
все все
все все
в) если x < 0 г) выбор
то z:=lg(-x) при с=0 : z:=1
иначе z:=sqrt(x+1) при с=1 : z:=x
все при с=2 : z:=3*x*x - 1/2
если z>=0 при с=3 : z:=x*x*x - 3*x/2
то F:=2*z+1 иначе z:=2*x**4 - 3*x/2
иначе F:=sin(z) все
все
д) если abs(x)+abs(y) < r е) если x>1
то z:=sqrt(x*x+y*y) то если y>1
иначе z:=max(abs(x), abs(y)) то v:=x+y
все иначе v:=x-y
все
ж) если (x-a)**2 +(y-b)**2 < r*r иначе если y>0
то z:=abs(x)+abs(y) то v:=y-x
иначе z:=x+y иначе v:=-x-y
все все
все
7.12.
б)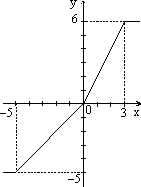 в)
в)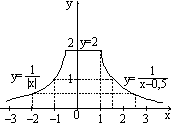 г)
г)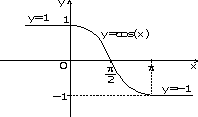 д)
д)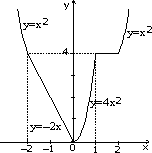
7.13. б) 81; в) 21; д) 11; е) 44.
7.14. б) 0; в) 13; д) 52; е) 14.
7.15.
б) алг Треугольник1(арг вещ a,b,UgolC, рез вещ c, UgolA, UgolB, S)
нач
ввод a, b, UgolC
c:=sqrt(a*a+b*b-2*a*b*cos(UgolC))
UgolA:=arcsin(a*sin(UgolC)/c)
UgolB:=arcsin(b*sin(UgolC)/c)
S:=b*c*sin(UgolA)/2
вывод c, UgolA, UgolB, S
кон
в) алг Треугольник2(арг вещ a,b,c, рез вещ Radius,UgolA)
нач вещ p
ввод a,b,c
p:=(a+b+c)/2
UgolA:=2*arctg(sqrt((p-b)*(p-c)/(p*(p-a))))*180/3.14
Radius:=a*b*c/(4*sqrt(p*(p-a)*(p-b)*(p-c)))
вывод Radius, UgolA
кон
г) алг Объем и Площадь Пирамиды(арг вещ a,UgolAGrad, рез вещ V, S)
нач вещ H,SBase,UgolARad
| H - высота пирамиды; SBase - площадь основания
ввод a,UgolAGrad
UgolARad:=UgolAGrad*3.14/180
SBase:=a*a*sqrt(3)/4
H:=a*sqrt(3)/6*tg(UgolARad)
V:=SBase*H/3
S:=SBase*(1+1/cos(UgolARad))
вывод V, S
кон
д) алг Объем и Площадь конуса(арг вещ RBig,RSmall,Ugol, рез вещ V, S)
нач вещ H,L
ввод RBig,RSmall,Ugol
H:=(RBig-RSmall)*tg(Ugol)
L:=(RBig-RadSmall)/cos(Ugol)
V:=1/3*3.14*H*(RSmall**2 + RBig**2 + RSmall*RBig)
S:=3.14*L*(RBig+RSmall)
вывод V, S
кон
е) алг Параметры пирамиды (арг вещ a,UgolA, рез вещ V, S, Sесtion)
нач вещ H
ввод a,UgolA
H:=a*sqrt(2)/2*tg(UgolA)
V:=1/3*a*a*H
Sесtion:=a*H*sqrt(2)/2
S:=a*a*(1+sqrt(2*tg(UgolA)**2+1))
вывод V, S, Sесtion
кон
7.16.
б) алг Количество положительных(арг вещ a,b,c, рез цел k)
надо | k - количество положительных чисел среди чисел a,b,c
нач
ввод a,b,c; k:=0
если a>0
то k:=k+1
все
если b>0
то k:=k+1
все
если c>0
то k:=k+1
все
вывод k
кон
в) алг Преобразование(арг рез вещ a,b)
надо |меньшее из a,b увеличено вдвое
нач
ввод a,b
если a>b
то b:=b*2
иначе a:=a*2
все
вывод a,b
кон
г) алг Подобие треугольников(арг вещ a,b,c,d, рез лог Otvet)
дано | a,b и c,d - катеты двух треугольников
надо | Otvet=да, если треугольники подобны
нач
ввод a,b,c,d
если (a*d=с*b) или (a*c=d*b)
то Otvet:=да
иначе Otvet:=нет
все
вывод Otvet
кон
д) алг Точки(арг вещ xA,yA,xB,yB,xC,yC, рез лит Otvet)
нач вещ DistA,DistB,DistC
ввод xA,yA,xB,yB,xC,yC
DistA:=sqrt(xA**2 + yA**2)
DistB:=sqrt(xB**2 + yB**2)
DistC:=sqrt(xC**2 + yC**2)
если (DistA < DistB) и (DistA < DistC)
то Otvet:="Это точка А"
иначе если DistB < DistC
то Otvet:="Это точка B"
иначе Otvet:="Это точка C"
все
все
вывод Otvet
кон
е) алг Принадлежность кольцу(арг вещ x,y,r1,r2, рез лог Otvet)
дано | r2>r1
надо | Otvet=да, если точка (x,y) принадлежит кольцу
| c внутренним радиусом r1 и внешним радиусом r2
нач
ввод x,y,r1,r2
если (x*x+y*y<=r2*r2) и (x*x+y*y>=r1*r1)
то Otvet:=да
иначе Otvet:=нет
все
вывод Otvet
кон
ж) алг Упорядочение по возрастанию(арг рез вещ a, b, c)
надо | числа a, b, c упорядочены по возрастанию
нач вещ t
ввод a, b, c
если a>b
то t:=a; a:=b; b:=t | меняются местами значения a и b
все
если a>c
то t:=a; a:=c; c:=t | меняются местами значения a и c
все
если b>c
то t:=b; b:=c; c:=t | меняются местами значения b и c
все
вывод a, b, c
кон