Назад
Зміст
Вперед
Задачі на зміну цифр натурального числа
Згадаємо, що десяткова система числення є позиційною. В позиційній системі числення значення кожної цифри залежить від її позиції – місця у числі.
Число 4131 насправді має такий склад:
4131=4*1000+1*100+3*10+1=4*103+1*102+3*101+1*100
Число 10, степені якого використовуються у цій формулі, називається
основою системи числення, а степені десятки – це вага цифри.
Приклад 1
Дано натуральне число. Замініть у ньому всі цифри 1 на 2.
Результат роботи програми
Змінні:
Вхідні:
Вихідні:
Проміжні:
-
c – остання цифра числа (цілого типу byte)
-
d – вага цифри у числі – 1, 10, 100, 1000, ... (цілого типу Longint)
Алгоритм
Скорочений алгоритм формування з введеного числа
n нового числа m такий:
- знаходимо c - останню цифру числа
n;
- якщо ця цифра 1, змінюємо її на 2, якщо ні, то не змінюємо;
- додаємо цю цифру в початок нового числа m (враховуючи вагу цифри
d);
- відкидаємо цифру з числа n;
- все це повторюємо, поки не закінчаться цифри у числі
n.
Щоб визначити формули, за якими будуть обчислюватись
m та d складемо таблицю для нашого прикладу:
| Змінна | c | m | d | n |
|---|
| Дія | Обчислення останньої цифри |
Накопичуємо цифру у початок числа | Вага цифри, степені числа 10 |
Відкидаємо останню цифру |
| Початкове значення | |
0 | 1 | 4131 |
| 1 виток циклу | 1 змінюємо на 2 |
2 | 10 | 413 |
| 2 виток циклу | 3 |
32=3*10+2 | 100 |
41 |
| 3 виток циклу | 1 змінюємо на 2 |
232=2*100+32 | 1000 |
4 |
| Останній виток циклу | 4 |
4232=4*1000+232 | 10000 |
0 |
| Формули | c:=n mod 10 |
m := c*d + m | d:=d*10 |
n:=n div 10 |
Аналізуючи третій стовпчик таблиці можна заповнити комірку, де буде формула для обчислення нового числа
m. Ясно, що для додавання цифри c у початок нового числа
m, потрібно множити її на вагу d, і цей добуток накопичувати у нове число
m.
Формула для обчислення степенів числа 10 нам відома. Можна записати її у четвертому стовпчику.
Тепер алгоритм докладніше:
- Спочатку потрібно ввести число оператором read(n).
- Нам потрібно сформувати нове число m. Ми будемо його накопичувати як суму, тому потрібно встановити початкове значення
m:=0.
- Використовуючи вагу цифри у числі d,
ми будемо її накопичувати як добуток, тому потрібно встановити початкове значення
d:=1.
- У вже відомий нам алгоритм перебору цифр числа, додамо два оператори (обчислення
m та d), які умовно можна назвати „формування нового числа”. Докладніше, у циклі будемо виконувати такі дії:
- оператор c:= n mod 10 обчислює останню
цифру числа;
- оператор if c=1 then c:=2 змінює цифру 1
на 2;
- оператор m:=m+c*d додає
знайдену цифру у початок нового числа, враховуючі її вагу;
- оператор d:=d*10 обчислює вагу
наступної цифри;
- оператор n:=n div 10 відкидає останню
цифру числа;
- Перевіряється умова n=0 – чи є ще цифри у числі?
- Якщо умова не вірна, тобто цифри у числі є, то виконується перехід на початок циклу (пункт 4).
- Якщо умова вірна, тобто цифр у числі немає, то цикл завершується і виконується перехід на оператор, що іде після циклу (пункт 5).
- Коли цикл закінчиться, тобто будуть видалені всі цифри числа
n, виводимо на екран знайдене нове число оператором writeln(m).
Блок–схема програми
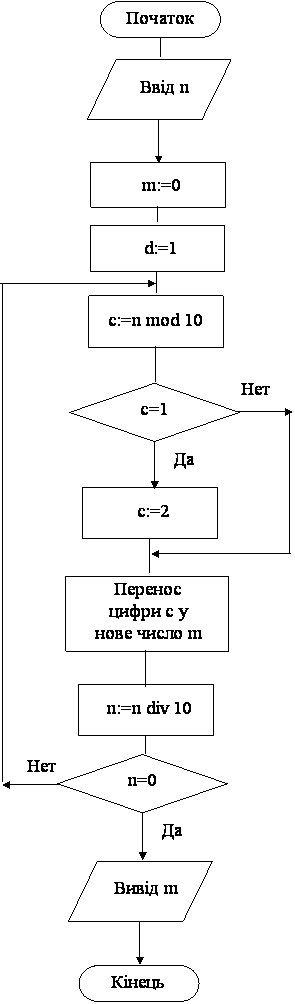
Програма
var n,m,d:longint; c:byte;
begin
read(n);
m:=0; d:=1;
repeat
c:=n mod 10;
if c=1 then c:=2;
m:=m+c*d; d:=d*10;
n:=n div 10;
until n=0;
writeln(m);
end.
|
Приклад 2
Дано натуральне число n. Вилучить у ньому всі 1.
Результат роботи програми
Змінні:
Вхідні:
Вихідні:
Проміжні:
-
c – остання цифра числа (цілого типу byte)
-
d – вага цифри у числі – 1, 10, 100, 1000, ... (цілого типу Longint)
Алгоритм
Алгоритм формування з введеного числа n нового числа
m без 1 відрізняється від алгоритму попередньої задачі тим, що оператори, які ми назвали „формування нового числа” виконуються тільки, коли цифра, яка переноситься у нове число не 1. Якщо цифра дорівнює 1, то ці оператори не виконуються і цифра в нове число не переноситься.
Тепер алгоритм докладніше:
- Спочатку потрібно ввести число оператором read(n).
- Встановимо початкове значення нового числа m:=0.
- Встановимо початкове значення ваги d:=1.
- У циклі будемо виконувати такі дії:
- Оператор c:= n mod 10 обчислює останню цифру числа.
- Якщо ця цифра не 1 (оператор if c<>1 then ), то переносимо її у нове число:
- оператор m:=m+c*d додає знайдену цифру у початок нового числа, враховуючі її вагу;
-
оператор d:=d*10 обчислює вагу наступної цифри.
- Оператор n:=n div 10 відкидає останню цифру числа
n.
- Перевіряється умова n=0 – чи є ще цифри у числі?
- Якщо умова не вірна, тобто цифри у числі є, то виконується перехід на початок циклу (пункт 4).
- Якщо умова вірна, тобто цифру числі немає, то цикл завершується і виконується перехід на оператор, що іде після циклу (пункт 5).
- Коли цикл закінчиться, тобто будуть видалені всі цифри числа n виводимо на екран знайдене нове число оператором
writeln(m).
Програма
var n,m,d:longint; c:byte;
begin
read(n);
m:=0; d:=1;
repeat
c:=n mod 10;
if c<>1 then
begin
m:=m+c*d; d:=d*10;
end;
n:=n div 10;
until n=0;
writeln(m);
end.
|
Приклад 3
Дано натуральне число n. Переверніть число.
Наприклад, з числа 3456 одержати 6543.
Результат роботи програми
Змінні:
Вхідні:
Вихідні:
Проміжні:
Алгоритм
Скорочений алгоритм формування з введеного числа
n нового числа m такий:
- знаходимо c - останню цифру числа
n;
- додаємо цю цифру в кінець нового числа m (для додавання цифри у кінець числа, потрібно число
помножити на 10 та додати цифру);
- відкидаємо цифру з числа n;
-
все це повторюємо, поки не закінчаться цифри у числі
n.
Щоб визначити формулу, за якою буде обчислюватись
m складемо таблицю для нашого прикладу:
| Змінна | c | m | n |
|---|
| Дія | Обчислення останньої цифри |
Накопичуємо цифру у початок числа | Відкидаємо останню цифру |
| Початкове значення | |
0 | 3456 |
| 1 виток циклу | 6 |
6 | 345 |
| 2 виток циклу | 5 |
65=6*10+5 | 34 |
| 3 виток циклу | 4 |
654=65*10+4 | 3 |
| Останній виток циклу | 3 |
6543=654*10+3 | 0 |
| Формули | c:=n mod 10 |
m:= m*10+c | n:=n div 10 |
Аналізуючи третій стовпчик таблиці можна заповнити комірку, де буде формула для обчислення нового числа
m. Ясно, що для додавання цифри c у кінець нового числа
m, потрібно число m помножити на 10 та додати до нього знайдену цифру
с.
Тепер алгоритм докладніше:
- Спочатку потрібно ввести число оператором read(n).
- Для формування нового числа m будемо
накопичувати його як суму, тому потрібно встановити початкове значення m:=0.
- У цьому прикладі у відомий нам алгоритм перебору цифр числа додамо один оператор (обчислення
m), який умовно можна назвати „формування перевернутого числа”. Докладніше, у циклі будемо виконувати такі дії:
- оператор c:= n mod 10 обчислює останню
цифру числа;
- оператор m:=m*10+c додає знайдену цифру
у кінець нового числа;
- оператор n:=n div 10 відкидає останню
цифру числа;
- Перевіряється умова n=0 – чи є ще цифри у числі?
- Якщо умова не вірна, тобто цифри у числі є, то виконується перехід на початок циклу (пункт 3).
- Якщо умова вірна, тобто цифр у числі немає, то цикл завершується і виконується перехід на оператор, що іде після циклу (пункт 4).
- Коли цикл закінчиться, тобто будуть видалені всі цифри числа
n, виводимо на екран знайдене нове число оператором writeln(m).
Програма
var n,m:longint; c:byte;
begin
read(n); m:=0;
repeat
c:=n mod 10;
m:=m*10+c;
n:=n div 10;
until n=0;
writeln(m)
end.
|
Приклад 4
Дано натуральне число. Допишіть цифру 5 на початок цього числа.
Наприклад, було 324, стало 5324.
Результат роботи програми
Змінні:
Вхідні:
Вихідні:
Проміжні:
-
d – вага цифри 5 у числі – 1, 10, 100, 1000, ... (цілого типу Longint)
-
x – для запам’ятовування числа n (цілого типу Longint)
Алгоритм
Щоб отримати нове число m, потрібно цифру 5 помножити на її вагу у новому числі (у прикладі на 1000) та до цього добутку додати введене число
n (у прикладі 5*1000+324=5324).
Задача зводиться до пошуку d ваги цифри 5 у новому числі. Для цього у циклі
d домножаємо на 10 стільки разів, скільки цифр у числі. Тобто:
- виконуємо оператор d:=d*10;
- відкидаємо цифру з числа n;
- все це повторюємо, поки не закінчаться цифри у числі
n.
Тепер алгоритм докладніше:
- Спочатку потрібно ввести число оператором read(n).
- Введене число n нам буде потрібно в остаточній формулі. Але ми будемо від нього відкидати цифри для пошуку ваги цифри 5 у новому числі. Тому це число потрібно запам’ятати оператором
x:=n.
- Ми будемо використовувати d - вагу цифри 5 у новому числі. Її потрібно накопичувати як добуток, тому потрібно встановити початкове значення
d:=1.
- У циклі знаходимо вагу цифри 5 у новому числі. Для цього будемо виконувати такі дії:
- оператор d:=d*10 обчислює вагу наступної
цифри;
- оператор n:=n div 10
відкидає останню цифру числа n;
- Перевіряється умова n=0 – чиє ще цифри у числі?
- Якщо умова не вірна, тобто цифри у числі є, то виконується перехід на початок циклу (пункт 4).
- Якщо умова вірна, тобто цифру числі немає, то цикл завершується і виконується перехід на оператор, що іде після циклу (пункт 5).
- Коли цикл закінчиться, обчислимо значення нового числа оператором
m:=5*d+x. У цій формулі використовуємо x замість n, тому що значення
n вже 0.
- Потім виводимо на екран знайдене нове число оператором
writeln(m).
Програма
var n,m,d,x:longint;
begin
read(n);x:=n;
d:=1;
repeat
d:=d*10;
n:=n div 10;
until n=0;
m:=5*d+x;
writeln(m);
end.
|
Варіанти задач
- Дано натуральне число. Змініть у ньому всі цифри
a на b.
- Дано натуральне число. Вилучить з нього всі цифри
a.
- Дано натуральне число. З’ясуйте, чи є воно паліндромом (перевернуте число дорівнює введеному).
- Дано натуральне число. Припишіть цифру a в початок цього числа.
- Дано натуральне число. Допишіть по двійці в початок та кінець цього числа.
- Дано натуральне число. Припишіть цифру a в початок та цифру
b у кінець цього числа.
- Дано натуральне число. Вилучити з нього всі цифри, що співпадають з останньою цифрою.
- Дано натуральне число. Вилучити з нього тільки першу цифру.
- Дано натуральне число. Вилучити з нього всі входження першої цифри.
- Дано натуральне число. Допишіть до нього таке ж саме число.
- Дано натуральне число n. Припишіть до нього число
m.
- Дано натуральне число n. Припишіть до нього число m в початок та кінець цього числа.
- Дано натуральне число. Вилучити з нього всі входження мінімальної цифри.
- Дано натуральне число. Вилучити з нього максимальну цифру. Якщо максимальних цифр декілька (39892), то вилучити останню максимальну(3982).
- Дано натуральне число. Сформуйте нове число, в якому перед кожною цифрою 1 вставлена цифра 0 (наприклад, було 3141 стало 301401).
- Дано натуральне число. Переставте його першу та останню цифри.
Назад
Зміст
Вперед

