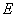 – середину
– середину
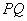 , через
, через
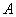 – середину
– середину
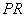 .
.
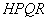 є рівнобедрений
прямокутний трикутник
є рівнобедрений
прямокутний трикутник
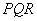 з гіпотенузою
з гіпотенузою
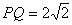 . Бічне ребро
. Бічне ребро
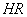 перпендикулярне до
площини основи і дорівнює 1.
Знайти величину кута і відстань між
мимобіжними прямими, одна з яких проходить
через точку
перпендикулярне до
площини основи і дорівнює 1.
Знайти величину кута і відстань між
мимобіжними прямими, одна з яких проходить
через точку
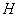 і середину ребра
і середину ребра
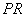 , а друга – через точку
, а друга – через точку
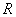 і середину
і середину
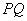 .
.
Позначимо через
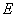 – середину
– середину
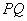 , через
, через
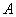 – середину
– середину
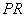 .
.
Тоді
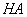 та
та
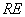 – мимобіжні прямі,
відстань і кут між якими і треба знайти за
умов:
– мимобіжні прямі,
відстань і кут між якими і треба знайти за
умов:
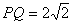 ,
,
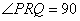 °, HR=1,
°, HR=1,

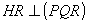 .
.
Проведемо через точку
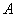 пряму
пряму
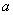 ||
||
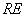 , а через точку
, а через точку
 пряму b||
пряму b||
 (у площині основи).
(у площині основи).
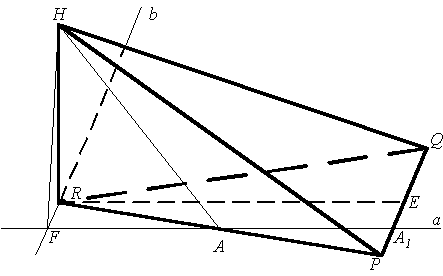
 - точка перетину прямих а
та b, А1 - точка
перетину прямих а та
- точка перетину прямих а
та b, А1 - точка
перетину прямих а та
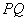 .
.
Згідно означення кута між мимобіжними прямими, менший з кутів HAF та HAA1 і буде шуканим.
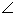 HAF - кут ∆HFA.
HAF - кут ∆HFA.
За умовою
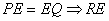 - медіана рівнобедреного трикутника
- медіана рівнобедреного трикутника
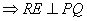 , але
, але
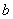 ||
||
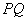 ,
,
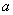 ||
||
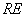
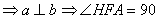 °
°
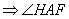 гострий кут прямокутного
гострий кут прямокутного
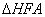
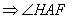 - шуканий.
- шуканий.
З ΔHFA:
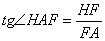 ,
,
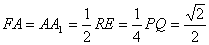 .
.
З ΔHRF:
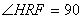 °,
°,
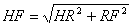 , де
, де
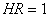 - за умовою.
- за умовою.
З
ΔRFA:
![]()
Тоді 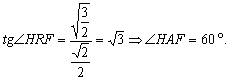
Тепер знайдемо відстань між вказаними
прямими. Очевидно, що в силу побудови,
шукана відстань буде дорівнювати відстані
від точки
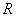 до площини
до площини
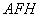 (адже
(адже
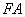 ||
||
![]() ||
||
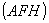 ).
).
Для знаходження цієї відстані розглянемо
тетраедр
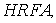 в якому
в якому
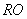 - шукана відстань і висота.
- шукана відстань і висота.
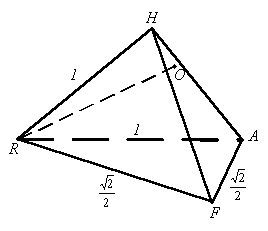
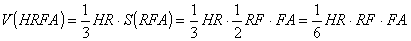
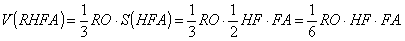
Враховуючи, що

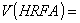
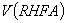 ,
,
маємо

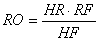 ,
,
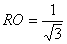 .
.
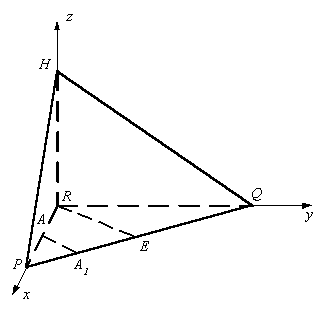 Про наведений
розв’язок впевнено можна сказати, що він
може бути виконаний лише 11- класниками. А
задача – то ж гарна! І так хочеться розв’язати
її з десятикласниками. Тут можуть стати у
пригоді вектори і координати. А саме:
виберемо систему координат так, щоб початок
координат співпадав з точкою
Про наведений
розв’язок впевнено можна сказати, що він
може бути виконаний лише 11- класниками. А
задача – то ж гарна! І так хочеться розв’язати
її з десятикласниками. Тут можуть стати у
пригоді вектори і координати. А саме:
виберемо систему координат так, щоб початок
координат співпадав з точкою
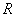 , сторона
, сторона
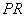 належала осі
абсцис,
належала осі
абсцис,
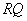 - осі ординат, а ребро
- осі ординат, а ребро
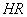 - осі аплікат.
- осі аплікат.
У вибраній системі координат встановимо
координати точок
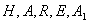 , враховуючи дані задачі.
, враховуючи дані задачі.
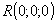 ,
,
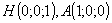 ,
,
![]() .
.
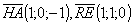 ;
;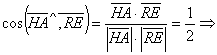 величина шуканого
кута 60°.
величина шуканого
кута 60°.
А відстань між прямими
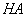 та
та
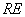 визначимо за відповідною
формулою як відстань від точки
визначимо за відповідною
формулою як відстань від точки
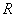 до площини
до площини
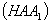 . Координати точки
. Координати точки
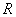 відомі. Залишилося записати рівняння
площини
відомі. Залишилося записати рівняння
площини
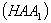 .
.
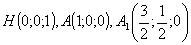
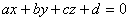 - загальне рівняння
цієї площини.
- загальне рівняння
цієї площини.
За
раніше побудованою схемою, маємо
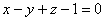 .
.
За формулою
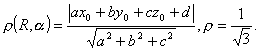
Відповідь: 60о та 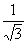 .
.
На мою думку другий спосіб простіший і
зручніший. Але, на жаль, його використання
ускладнюється, якщо за умовою задачі в
основі заданої піраміди лежатиме не
прямокутний трикутник. Наприклад, як у
наступній задачі, що підкреслює доцільність
розв’язування задач різними способами.
ДОВІДКАПро різні методи розв’язування задачі говорять тоді, коли для цих розв’язань характерні системи понять і міркувань з різних великих розділів математичної науки, наприклад, методи геометричних місць, координатний, векторний, алгебраїчний та інші. Коли йдеться про розв’язання однієї і тієї самої задачі за допомогою різних методів або прийомів, говорять про різні способи розв’язання. Векторний метод розв’язання стереометричних задач пов’язаний з використанням властивостей векторів. Розв’язуючи задачу векторним методом, спочатку подані в задачі співвідношення перекладають на “мову векторів”, і, нарешті, від мови векторів знову переходять до мови геометрії. Якщо, розв’язуючи геометричну задачу оперують координатами окремих точок, рівняннями ліній або поверхонь, то використовують координатний метод. Координатний метод часто поєднують з векторним, розглядаючи вектори, задані своїми координатами. Раціональність розв’язання стереометричної задачі координатним методом значною мірою залежить від того, як розглядувану фігуру розмістити відносно координатних осей. Найзручніше цим методом користуватись тоді, коли йдеться про фігури, що мають прямий тригранний кут. У цьому разі осі координат доцільно розмістити в напрямі ребер тригранного кута. Але не тільки такі задачі можна розв’язувати координатним методом. |