Тема уроку: "Поняття рекурсії.
Розв'язування задач на складання алгоритмів з використанням рекурсії."
Дати поняття про рекурсію,
оформлення підпрограм з рекурсією мовою програмування Паскаль.
Тип уроку: Практичний.
Чи траплялось Вам колись зазирнути у дзеркало, напроти якого стоїть таке саме
дзеркало? Не правда дивна картина? В першому дзеркалі ми побачимо відображення
із протилежного дзеркала, в якому, в свою чергу, видно зображення першого
дзеркала і т.д. Коли скінчиться цей процес? А жартівливий віршик "У попа
була собака..."?
В математиці часто зустрічаються такі розрахунки, коли наступне значення величини
обчислюється через попереднє. Наприклад, для того, щоб обчислити значення
степеню x^n необхідно знати значення x^(n-1), для чого в свою чергу необхідно
знати значення x^(n-2) і т.д. Якщо спробувати запрограмувати цей процес, не
порушуючи логіку міркувань та оформлюючи його підпрограмою (наприклад, функцією),
нам прийдеться для обчислення значення xn викликати функцію обчислення степеню
x^(n-1) і помножити це значення на величину х. Тобто ми приходимо до такого
явища, як виклик підпрограми в середині самої підпрограми.
Рекурсією називається така ситуація, коли підпрограма (процедура або
функція) викликає сама себе.
Типова конструкція рекурсивної процедури повинна мати наступний вигляд:
Procedure Rec (t:integer); Begin <Дії на початку рекурсії> If <Перевірка умови> Then Rec(t+1); <Дії на виході з рекурсії> End;Саме головне при написанні рекурсії усвідомити, як правильно задати умову, яка буде заглиблювати нас у рекурсію або, навпаки, виводити з неї.
Розглянемо приклад рекурсивного виклику на обчисленні степеня числа х^n, де х - будь-яке дійсне число, а n - ціле, додатне число. Очевидно, що
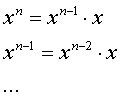
Постає питання, коли і як припинити цей процес? В даному випадку зупинкою для обчислень буде обчислення x0, так як відомо, що нульова степінь будь-якого числа дорівнює 1. Тобто рекурсивна функція для обчислення степеня числа буде мати наступний вигляд:
Function Step(x:real; n:integer):real: Begin If n = 0 then Step:=1 else Step:=Step(x,n-1)*x; End;Проаналізуємо роботу цієї функції на прикладі знаходження значення 23. При першому виклику функції значення змінних буде дорівнювати відповідно:
x = 2
n = 3.
Так як значення n не дорівнює 0 спрацює гілка else, тобто почне виконуватись такий оператор
Step:=Step(x,n-1)*x;
де x буде дорівнювати 2, і n - теж 2.
Цей оператор містить виклик функції step, тому виконання підпрограми перерветься і виконається виклик тієї ж самої функції step, але з параметрами x=2 та n=1. При виконанні повторного виклику функції ситуація повториться, так як n поки ще не дорівнює 0 і тільки на четвертому виклику функції step параметр n досягне нульового значення, після чого спрацює гілка then, яка присвоїть значення функції 1.
В даній найпростішій рекурсії ніякі дії при вході в рекурсію не відбуваються, але при виході з рекурсії необхідно знати точки, з яких здійснювався вхід в чергову функцію, щоб мати можливість повернутися в них. Ці точки виклику запам'ятовуються у спеціалізованій пам'яті, що зветься стек, і потім по черзі являються тими точками повернення, які використовує система при зворотному русі з рекурсії.
Очевидно, що виконання рекурсії є досить складним процесом, який крім того вимагає суттєвих витрат додаткових ресурсів (що найменше пам'яті). Тому використання рекурсії не рекомендується в тих випадках, коли вона просто замінюється ітеративним процесом (як в наведеному прикладі). Однак, існує велика кількість досить складних алгоритмів, які без використання рекурсії мають дуже заплутану логіку роботи.
З чисто учбовою метою покажемо, як розв'язувати деякі задачі за допомогою рекурсії, хоча наполягаємо на тому, що більшість із запропонованих завдань можна виконати без використання рекурсії. Та... Щоб зрозуміти рекурсію, треба зрозуміти рекурсію...
Отже задачі.
Задача № 440.
Умова: Використовуючи підпрограму обчислення факторіалу, розробити програму обчислення суми факторіалів усіх цілих чисел від 1 до 10.
Функція обчислення факторіалу є чи не найстандартнішою, яку приводять в усіх підручниках для пояснення явища рекурсії. Зробимо це й ми.
Очевидно, що
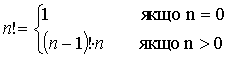
Тоді вихідна програма буде мати наступний вигляд:
Program Example_440;
Uses crt; {Підключення бібліотеки}
Function Factorial (n:integer):longint;
Begin
if n=0
then Factorial:=1
else Factorial:=Factorial(n-1)*n;
End;
Var Rez:longint;
i:byte;
Begin
Clrscr;
Rez:=0;
For i:=1 to 10 do
begin
Rez:=Rez+Factorial(i);
end;
writeln('Rezultat -> ',Rez);
Readkey;
End.
Задача № 495.
Умова: Знайти найбільший спільний дільник двох натуральних чисел n
та m за алгоритмом Евкліда:
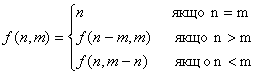
В даному випадку умовою виходу з рекурсії буде рівність двох чисел n=m.
Написання самої програми, на наш погляд, являється тривіальним:
Program Example_495;
Uses crt; {Підключення бібліотеки}
Function Evklid (n,m:integer):integer;
begin
if n=m
then Evklid:=n
else
if n>m
then Evklid:=Evklid(n-m,m)
else Evklid:=Evklid(n,m-n);
end;
Var x,y:integer;
Begin
Clrscr;
writeln ('Введіть два числа: ');
readln (x,y);
writeln ('НОД -> ',Evklid(abs(x),abs(y)));
Readkey;
End.
Задача № 498.
Умова: Обчислити значення функції Аккермана для двох невід'ємних
цілих чисел n та m, де:
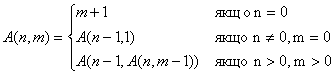
На наш погляд, реалізація запропонованої рекурсивної функції являється тривіальною,
тому наводимо текст програми без пояснень:
Program Example_498;
Uses crt; {Підключення бібліотеки}
Function A(n,m:word):word;
Begin
if n=0
then A:=m+1
else
if (n<>0) and (m=0)
then A:=A(n-1,1)
else A:=A(n-1,A(n,m-1));
End;
Var x,y:word;
Begin
Clrscr;
writeln ('введіть два числа: ');
readln (x,y);
writeln ('Результат обчислень -> ',A(x,y));
Readkey;
End.
Задача № 500.
Умова: Обчислити кількість комбінацій з n різних елементів
по m, тобто кількість неупорядкованих підмножин з m елементів,
що належать заданій множині з n елементів , скориставшись залежністю:
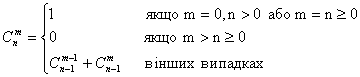
Програма, що виконує запропонований алгоритм, має наступний вигляд:
Program Example_500;
Uses crt; {Підключення бібліотеки}
Function C (n,m:word):longint;
Begin
if ((m=0) and (n>0)) or ((m=n) and (n>=0))
then C:=1
else
if (m>n) and (n>=0)
then C:=0
else C:=C(n-1,m-1)+C(n-1,m);
End;
Var x,y:word;
Begin
clrscr;
writeln ('Введіть два числа: ');
readln(x,y);
writeln ('Кількість комбінацій з ',x,' по',y,' -> ',C(x,y));
readkey;
End.