Тема уроку: "Методи створення рухомих графічних об'єктів засобами мови Паскаль"
Мета уроку: показати можливості створення рухомих графічних об'єктів та простих мультиплікаційних зображень засобами мови Паскаль на прикладах розв'язання задач.
Тип уроку: Практичний.
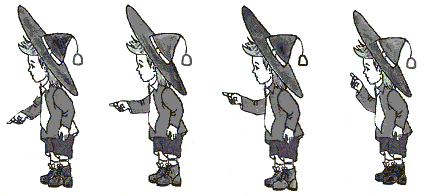
Щоб почати роботу над створення простішого "мультика" (зображення, що рухається), спочатку розберемося, як воно створюється в реальних умовах. Всі знають, що художник мультиплікатор малює серію зображень, в кожному з яких показується один і той же рух з ледь помітними змінами. Наприклад так, як це показано на наступному малюнку.

Тепер, якщо зображення швидко змінювати одне за одним, ми не помічаємо зміну
малюнків, а бачимо рух цього персонажу (в даному випадку Незнайко піднімає руку).
Поміркуємо, як відтворити послідовність схожих об'єктів на екрані монітору.
Перше, що спадає на думку, це намалювати зображення, затримати його трохи на
екрані, витерти зображення (очистити екран) та вивести нове зображення з ледь
помітними змінами. При достатньо великій швидкості малювання око людини не помітить
зміни малюнків і їй буде здаватися, що об'єкт рухається. Розв'яжемо таким методом
наступну задачу.
Задача № 629.
Умова: "Годинник". Змоделювати рух годинної та хвилинної стрілок.
Якщо змоделювати роботу годинника в реальному часі, то наочність програми буде
невеликою, тому що рух стрілок буде ледь помітним. Тому зробимо імітацію роботи
годинника, тобто хвилинна стрілка буде рухатися достатньо швидко, а рух годинникової
стрілки буде залежати від хвилинної.
На початку роботи з'ясуємо, з яких елементів складається годинник. По-перше,
це круг з поділками, а, по-друге, два відрізка різної довжини, що імітують стрілки
(стрілки можна зробити і більш складними). Круг являється нерухомим об'єктом,
тому він малюється статично з абсолютними координатами центру та радіусом, а
стрілки рухаються, причому переміщується тільки один кінець стрілки-відрізка,
а другий теж являється статичним (центр круга).
Формули, за якими обчислюються координати рухомого кінця стрілки, відомі учням
з курсу математики (поворот точки на заданий кут відносно нерухомого центру
з координатами x0, y0). Тому наводимо їх тут без пояснень:
x = x0 + L*cosa
y = y0 + L*sina
де L - відстань, на якій знаходиться точка від центру повороту,
a - кут, на який повертається точка.
Зверніть увагу тільки на те, що в програмі друга формула замість знаку "-"
буде містити знак "+", тому що екранні координати мають направленість
осей, зворотну до реальних Декартових координат (на екрані значення координати
Y збільшується в напрямку зверху вниз).
Малювання поділок на циферблаті виконується теж за допомогою вище наведених
формул
Програма, що реалізує запропонований алгоритм, наведена нижче. Зверніть увагу,
що в цій програмі
L_min, L_time - довжини хвилинної та годинникової стрілок відповідно;
Color_min, Color_time - кольори хвилинної та годинникової стрілок
відповідно;
R - радіус циферблату годинника;
х_centr, y_centr - координати центра екрану (визначаються у відповідності
до поточної роздільної здатності за допомогою функцій getmaxx та getmaxy;
х_min, y_min - координати рухомого кінця хвилинної стрілки;
х_time, y_time - координати рухомого кінця годинникової стрілки;
Ang_min, Ang_time - кути повороту хвилинної та годинникової стрілок
відповідно.
Рух стрілок по циферблату здійснюється за рахунок постійного їх перемалювання
то активним кольором малювання стрілки, то кольором тла ("затирання"
зображення). Програма завершується після натискання будь-якої клавіші за рахунок
використання циклу repeat until keypressed.
Program Example_629;
Uses crt,graph; {Підключення бібліотек}
const L_min=174;
L_time=145;
Color_min=white;
Color_time=white;
R = 200;
var gd,gm:integer;
S:string[2];
x_centr, y_centr:integer;
i,x_min,y_min:integer;
x_time,y_time:integer;
Ang_min,Ang_time:real;
begin
{Ініціалізація графічного режиму}
gd:=VGA; gm:=VGAHi;
InitGraph (gd,gm,'egavga.bgi');
{Визначення центра екрану}
x_centr := getmaxx div 2;
y_centr := getmaxy div 2;
{Малювання статичної частини малюнку}
SetColor(brown);
SetFillStyle(1,brown);
{Малювання циферблату коричневого кольору}
FillEllipse(x_centr,y_centr,R,R);
Ang_time:=-90;
{Встановлення кольору малювання, стилю та вирівнювання тексту}
SetColor(yellow);
SetTextJustify(CenterText, CenterText);
SetTextStyle(DefaultFont, HorizDir, 2);
{Малювання поділок жовтого кольору та цифр}
for i:=1 to 12 do
begin
Ang_time:=Ang_time+30;
x_time:=round(x_centr+185*cos(Ang_time*pi/180));
y_time:=round(y_centr+185*sin(Ang_time*pi/180));
str(i,S);
OutTextXy(x_time,y_time,S);
end;
{Малювання ходу годинника}
Ang_min:=-90;
Ang_time:=-90;
repeat
x_time:=round(x_centr+L_time*cos(Ang_time*pi/180));
y_time:=round(y_centr+L_time*sin(Ang_time*pi/180));
SetColor(Color_min);
Line(x_centr,y_centr,x_time,y_time);
x_min:=round(x_centr+L_min*cos(Ang_min*pi/180));
y_min:=round(y_centr+L_min*sin(Ang_min*pi/180));
SetColor(Color_min);
Line(x_centr,y_centr,x_min,y_min);
Delay(10000); {Затримка зображення на екрані}
SetColor(brown);
Line(x_centr,y_centr,x_time,y_time);
Line(x_centr,y_centr,x_min,y_min);
Ang_min:=Ang_min+6;
Ang_time:=Ang_time+0.5;
until keypressed;
readkey;
CloseGraph;
end.
Запропонований метод побудови мультиплікаційних об'єктів являється найпростішим,
але якщо об'єкт, що рухається, має більші лінійні розміри, ніж в запропонований
задачі, він буде суттєво миготіти на екрані. Тому існує інший підхід до розв'язку
цієї задачі. В цьому випадку пропонується наступний алгоритм:
а) намалювати бажаний об'єкт;
б) запам'ятати область екрана, з виведеним малюнком;
в) відновити екран в місці, де був малюнок (тобто стерти малюнок);
г) вивести малюнок на нове місце і т.д.
Цей підхід дуже схожий на попередній варіант, але має суттєві переваги в тому,
що не потребує багаторазового перемалювання малюнку. Об'єкт створюється один
раз, зберігається його копія, а потім виводиться в потрібному місці.
Для зберігання намальованого фрагмента необхідно використовувати оперативну
пам'ять, причому так як ми не знаємо розміри об'єкта на початку програми, пам'ять
необхідно запрошувати у системи безпосередньо під час роботи програми. Це можна
зробити тільки використовуючи динамічну пам'ять за допомогою наступних підпрограм:
1. GetImage(x1,y1,x2,y2,BitMap) - зберігає образ вказаної прямокутної
області екрана в динамічній області пам'яті.
В цій підпрограмі
х1, y1, x2, y2 - координати лівого верхнього та
правого нижнього кутів прямокутної області екрана, образ якої ми хочемо зберегти;
BitMap - адреса області пам'яті, в якій ми зберігаємо об'єкт.
2. PutImage (x,y,BitMap,Mode) - відновлює збережений образ прямокутної
області.
Тут x, y - координати верхнього лівого кута області екрана, в
яку ми хочемо помістити зображення;
BitMap - адреса пам'яті, в якій було збережено зображення;
Mode - режим накладання зображення на екран. Режимів накладання існує
5 (від 0 до 4), але самими цікавими для нас являються CopyPut (0) - заміщення
новим об'єктом старого зображення та XOR (1) - "витирання"
старого об'єкта.
Крім цих основних підпрограм при використанні оперативної пам'яті для збереження
об'єкта нам знадобляться ще дві. Перша допомагає визначити об'єм необхідної
пам'яті в байтах для збереження прямокутного малюнку, а друга запрошує у системи
відповідну області пам'яті. Їх використовують разом наступним чином:
{визначається необхідний розмір області пам'яті}
Size := ImageSize(x1,y1,x2,y2);
{у системи запрошується оперативна пам'ять}
GetMem(BitMap,Size);
де x1, y1, x2, y2 - координати прямокутної області
екрану, де знаходиться малюнок;
Size - розмір необхідної пам'яті (змінна цілого типу);
BitMap - адреса оперативної пам'яті, що виділяється системою (змінна
типу вказівник для збереження адреси).
Покажемо тепер, як за допомогою цих підпрограм можна побудувати об'єкт, що рухається,
на прикладі наступної задачі.
Задача № 638 (1).
Умова: "Баскетбол". Зобразити на екрані відбивання від підлоги,
стін та стелі м'яча, що зображається зафарбованим кругом. Для спрощення алгоритму
траєкторію руху м'яча вважати ламаною лінією. Силою тертя повітря знехтувати.
У наведеній нижче програмі описані наступні константи:
- R являється радіусом м'яча,
- Time - час затримки зображення на екрані (підбирається емпіричним шляхом
в залежності від типу ПЕОМ).
Крім того використовуються наступні змінні:
- x та y вказують на координати лівого верхнього кута області екрана,
куди виводиться, а потім звідки витирається зображення;
- Size та BitMap - використовуються для збереження зображення
в оперативній пам'яті (дивись вище);
- Step_x та Step_y - задають крок, на який пересувається об'єкт
при кожному наступному перемалюванні (теж підбирається емпірично в залежності
від типу ПЕОМ).
Перший м'яч малюється в лівому верхньому кутку екрану і напрямок його руху -
зверху вниз, зліва направо, тому початкові координати області зображення x та
y дорівнюють 0, а обидва кроки додатні. Далі, якщо об'єкт долітає до границі
екрана, то крок змінюється на протилежний за знаком, і об'єкт починає рухатись
в зворотному напрямку.
Програма, що реалізує запропонований алгоритм, має наступний вигляд:
Program Example_638_1;
uses crt,graph;
const R=20;
Time = 1000;
var gd,gm:integer;
x,y:integer;
Size:integer;
Step_x,Step_y:integer;
BitMap:pointer;
begin
x:=0; y:=0;
Step_x:=5;
Step_y:=5;
gd:=VGA; gm:=VGAHi;
InitGraph (gd,gm,'egavga.bgi');
SetColor(brown);
SetFillStyle(1,brown);
FillEllipse(R,R,R,R);
size:= ImageSize(0,0,2*R,2*R);
GetMeM(BitMap,Size);
GetImage(0,0,2*R,2*R,BitMap^);
repeat
delay(Time);
PutImage(x,y,BitMap^,1);
x:=x+Step_x;
y:=y+Step_y;
if (x+2*R >= getmaxx) or (x<=0)
then Step_x:=-Step_x;
if (y+2*R >= getmaxy) or (y<=0)
then Step_y:=-Step_y;
PutImage(x,y,BitMap^,1);
until keypressed;
readkey;
CloseGraph;
end.
Третій метод, що дозволяє ще зменшити миготіння мультиплікаційного об'єкта
на екрані, це використання графічних сторінок. Відомо, що при ініціалізації
графічного режиму ми задаємо два параметри:
Gd - тип графічного адаптера (CGA, EGA, VGA і т.д.);
Gm - режим роботи графічного адаптера.
В залежності від цих параметрів на екран можна виводити зображення з різною
роздільною здатністю та палітрою. Крім того, існують деякі режими, що підтримують
кілька графічних сторінок, кожна з яких може містити різні зображення. В один
момент часу ми можемо бачити тільки одну сторінку, але в той самий момент можемо
готувати складне зображення на інших сторінках і потім миттєво виводити їх на
екран, зменшуючи таким чином миготіння (людина не бачить малювання окремих деталей
пейзажу).
Один з таких режимів Gm=VGAMed дозволяє програмісту виводити 16-кольорове
зображення з роздільною здатністю 640 на 350 пікселів, при цьому він підтримує
дві графічних сторінки.
Для того, щоб скористатися цими сторінками, ми можемо в програмі застосувати
дві підпрограми:
SetActivePage (Page) - задається номер активної сторінки (Page),
тобто сторінки, на якій в даний момент буде будуватися зображення;
SetVisualPage (Page) - задається номер візуальної сторінки, тобто тієї
сторінки, що являється видимою в даний момент.
В запропонованому режимі існує тільки дві сторінки, що мають номера 0 та 1,
тому зміну сторінок можна виконувати змінною Page, що буде змінюватись за наступним
законом:
Page := 1-Page,
причому активна сторінка стає видимою тільки після того, як на ній повністю
побудовано нове зображення.
Покажемо застосування цього прийому побудови зображення, що рухається, на наступній
задачі.
Задача № 627 (модифікована).
Умова: Скласти програму, яка виводитиме на екран рух тіла, кинутого під
кутом до горизонту. Опором повітря знехтувати.
Програма, що реалізує описаний алгоритм, наведена нижче. В ній використовуються
наступні константи:
G = 9.8 -
Color - колір тіла, що кинуто;
Radius - радіус тіла;
Time - затримка зображення на екрані (підбирається емпіричним шляхом
в залежності від типу ПЕОМ).
Program Example_627_m;
uses crt,graph;
const g=9.8;
Color = 2;
Radius = 20;
Time = 500;
var gd,gm:integer;
Page:byte;
Vx,Vy,X,Y:real;
begin
gd:=VGA; gm:=VGAMed;
InitGraph (gd,gm,'egavga.bgi');
Vx:=40; Vy:=30; X:=15; Y:=160;
SetColor (Color);
SetFillStyle(1,Color);
repeat
SetActivePage (Page);
ClearDevice;
Circle (round (X),round (Y),Radius);
FloodFill(round(X),round(Y),Color);
SetVisualPage (Page);
Page:=1-Page;
Delay (Time);
X:=X+Vx*0.1;
if Vy<>0 then Y:=Y-Vy*0.1;
Vy:=Vy-g*0.1;
Until keypressed;
CloseGraph;
end.
Домашнє завдання: