| [ домой ] | [ следующий ] [ начало главы ] [ предыдущий ] | [ содержание ] |
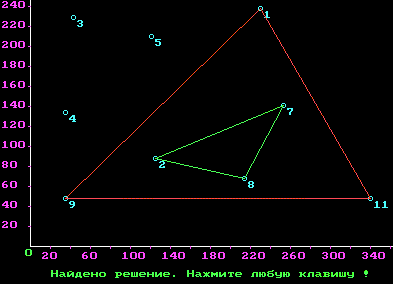
Пример 8.11. Программа рисует прямоугольную систему координат, отображает в ней заданное множество точек и строит все возможные пары треугольников с вершинами в этом множестве такие, чтобы один треугольник лежал строго внутри другого.

Для работы программы необходимо предварительно создать в текущем каталоге
текстовый файл dan.dat, содержащий координаты точек множества. Файл
должен иметь структуру:
x1 y1
x2 y2
... xn yn
, где 0 < xi <
400, 0 < yi <
600.
Пример файла dan.dat, содержащего координаты десяти точек:
20 20 150 40 90 300 500 400 50 380 110 130 370 290 300 140 70 60 500
170
Пустых строк в файле dan.dat быть не должно.
Program Triangles; {Составил студент Тезадов С., 1 к. мат. фак. КБГУ}
Uses Crt,Graph;
Const DemoN = 10;
DemoX: array [1..DemoN] of Integer = (20,150,90,500,50,110,370,300,70,500);
DemoY: array [1..DemoN] of Integer = (20,40,300,400,380,130,290,140,60,170);
Var X, Y : Array[1..50] of Integer; {координаты точек множества}
InX, InY : Array[1..50] of Integer; {координаты вершин внутренних}
Flag : Boolean; {треугольников}
Ch : Char;
Coord, Num : String;
i, j, k, p, i1, j1, k1, n, n1 : Integer;
GrDriver, GrMode, GrError : Integer;
{--------------------------}
Procedure InputOutput; {Описание процедуры считывания координат точек
множества из текстового файла dan.dat в массивы
X и Y и вывода точек на графический экран }
Var f : Text;
a,b : Real;
Begin
Assign(f, 'dan.dat'); {установление связи между физическим }
{файлом dan.dat и файловой пеpеменной f}
{$I-} {- отключаем автоматическую проверку существования файла}
Reset(f); i:=0; {открытие файла f для чтения}
{$I+}
If IOResult = 0 then begin {если файл существует}
While not eof(f) do {цикл "пока не будет достигнут конца файла"}
begin Read(f,a,b); Inc(i); {считывание из файла f пары координат}
X[i]:=Trunc(a-1); Y[i]:=Trunc(428-b) {преобразование декартовых}
end; {координат в координаты графического экрана}
n:=i; {n - количество введенных точек множества}
Close(f); {закрытие файла f}
end
Else begin {если файла не существует, то используем множество точек,}
n := DemoN; {заданное в DemoN, DemoX, DemoY.}
For i:=1 to DemoN do begin
x[i] := DemoX[i];
y[i] := 428 - DemoY[i];
end;
end;
SetColor(LightCyan);
OutTextXY(200,30,'ИСХОДНОЕ МНОЖЕСТВО ТОЧЕК');
For i:=1 to n do {рисование и нумерация точек множества}
begin Circle(X[i], Y[i], 2);
Str(i, Num); OutTextXY(X[i]+4, Y[i]+3, Num)
end;
Ch:=ReadKey; ClearViewPort; {очистка графического окна}
End; {of InputOutput}
{--------------------------}
Procedure Drawing_Axes; {описание процедуры рисования осей координат}
Begin SetColor(White);
MoveTo(30,0); LineTo(30,430); LineTo(639,430); {оси ОХ,OY}
OutTextXY(27,0,'^'); OutTextXY(630,427,'>'); {стрелки осей OX, OY}
SetColor(LightGreen);
OutTextXY(18,0,'y'); OutTextXY(630,434,'x');
OutTextXY(25,433,'0');
SetColor(LightMagenta); {установка розового цвета}
For i:=1 to 20 do {нанесение делений и числовых отметок на ось OY}
begin Str(20*(21-i), Coord); j:=i*20+10;
OutTextXY(2, j-5, Coord);
Line(28, j, 30, j)
end;
For i:=1 to 29 do {нанесение делений и числовых отметок на ось OX}
begin Str(20*i,Coord); j:=i*20+30;
If Odd(i) then OutTextXY(j-8, 436,Coord); Line(j,430, j,432)
end;
SetViewPort(31,4,630,429,FALSE) {установка текущего графического окна}
End; {of Drawing_Axes}
{--------------------------}
Function Inside(i, j, k, p : Integer ) : Boolean;
{функция Inside возвращает TRUE, если точка с номером p
находится внутри треугольника с вершинами в точках i, j, k}
Var S1, S2 : Real;
{---------------------------------------------------}
Function Area(x1, y1, x2, y2, x3, y3 : Real) : Real;
{функция вычисления площади треугольника}
{с вершинами в точках (x1,y1), (x2,y2), (x3,y3)}
Begin Area:=abs((x1*(y2-y3)+x2*(y3-y1)+x3*(y1-y2))/2)
End; {of Area}
{--------------------------------------------------------}
Begin S1:=Area(X[i], Y[i], X[j], Y[j], X[k], Y[k]);
{S1 - площадь треугольника с вершинами в точках i, j, k}
S2 := Area(X[i], Y[i], X[j], Y[j], X[p], Y[p]) +
Area(X[j], Y[j], X[k], Y[k], X[p], Y[p]) +
Area(X[k], Y[k], X[i], Y[i], X[p], Y[p]);
{S2 - сумма площадей трех треугольников с вершинами
в точках (i,j,p), (j,k,p), (i,k,p) }
Inside:=S1>S2 - 0.001
End; {of Inside}
{--------------------------}
Procedure Triangle(x1, y1, x2, y2, x3, y3 : Integer; Color : Byte);
Begin {описание процедуры рисования треугольника цвета Color}
SetColor(Color);
Line(x1, y1, x2, y2);
Line(x2, y2, x3, y3);
Line(x3, y3, x1, y1)
End; {of Triangle}
{--------------------------}
BEGIN
GrDriver:=Detect;
InitGraph(GrDriver, GrMode, 'C:\TP\BGI');
GrError:= GraphResult;
If GrError<>GrOk then begin WriteLn(' Ошибка графики!'); Halt end;
Drawing_Axes; {вызов процедуры рисования осей координат}
InputOutput; {вызов процедуры ввода и вывода исходных данных}
Flag:=FALSE;
For i:=1 to n -2 do {циклы по номерам вершин внешнего треугольника}
For j:=i+1 to n -1 do
For k:=j+1 to n do
begin
SetColor(LightCyan); {установка яркоголубого цвета}
For p:=1 to n do {рисование и нумерация точек множества}
begin Circle(X[p], Y[p], 2); {рисование точки}
Str(p, Num);
OutTextXY(X[p]+4, Y[p]+3, Num) {вывод номера точки}
end;
n1:=0; {занесение координат точек, находящихся
внутри треугольника, в массивы InX и InY}
For i1:=1 to n do
begin
If (i1<>i) and (i1<>j) and (i1<>k) and Inside(i,j,k,i1)
then begin Inc(n1); InX[n1]:=X[i1]; InY[n1]:=Y[i1]
end;
end;
If n1>=3 then {если число точек внутри треугольника не меньше трех,}
begin Flag:=TRUE; {то строятся внутренние треугольники}
For i1:=1 to n1-2 do {циклы по номерам вершин внутренних}
For j1:=i1+1 to n1-1 do {треугольников}
For k1:=j1+1 to n1 do
begin {рисование внешнего треугольника красным цветом}
Triangle(X[i],Y[i],X[j],Y[j],X[k],Y[k],LightRed);
{рисование внутреннего треугольника зеленым цветом}
Triangle(InX[i1],InY[i1],InX[j1],InY[j1],InX[k1],InY[k1],
LightGreen);
OutTextXY(80,450,'Найдено решение. Нажмите любую клавишу!');
Ch:=ReadKey;
SetColor(Black); {"стирание" сообщения}
OutTextXY(80,450,'Найдено решение. Нажмите любую клавишу!');
{"стирание" внутреннего треугольника}
Triangle(InX[i1],InY[i1],InX[j1],InY[j1],InX[k1],InY[k1],
Black)
end {конец циклов по номерам вершин внутренних треугольников}
end;
{"стирание" внешнего треугольника}
Triangle(X[i], Y[i], X[j], Y[j], X[k], Y[k], Black)
end; {конец циклов по номерам вершин внешнего треугольника}
SetColor(White);
If not Flag then OutText('Для данного множества нет решений задачи')
else OutText('РАБОТА ПРОГРАММЫ ЗАВЕРШЕНА');
OutTextXY(80,450,' Нажмите любую клавишу ...');
Ch:=ReadKey;
CloseGraph {закрытие графического режима}
END.
| [ домой ] | [ следующий ] [ начало главы ] [ предыдущий ] | [ содержание ] |