Назад
Зміст
Вперед
Задачі на обчислення елементів послідовності через попередні елементи
Ми обчислювали елементи послідовності за формулою таким чином: підставляли номер елемента послідовності у формулу та отримували значення елемента.
Але таким чином можна обчислити елементи не для всіх послідовностей. Якщо у формулі для обчислення елемента
ai присутній один чи декілька попередніх елементів (ai-1
або ai-2), або формула для обчислення елементу послідовності містить піднесення до степеня чи факторіал, або словесно вказується, як обчислюється „наступний” елемент через „попередній”, то цей алгоритм не підходить.
Наприклад, необхідно обчислити 5 чисел: a1=3, ai=ai-1+5, i=2,3,…5. Нам необхідно обчислити елементи послідовності через один попередній (бо у формулі справа від знака „=” тільки
ai-1). Підставляємо значення i=2,3,…5 у формулу. Отримаємо:
a1=3
a2=a1+5=3+5=8
a3=a2+5=8+5=13
a4=a3+5=13+5=18
a5=a4+5=18+5=23
Правило обчислення елементів послідовності через один попередній
- Для значень елементів послідовності досить одної змінної (a). Порядкові номери елементів в програмі не використовуються.
- Перед циклом потрібно присвоїти перше значення змінній (a). Воно буде „попереднім” (для приклада
a:=3).
- У циклі for i:=2 to n+1 do (цикл від 2, бо одне число вже обчислили):
- виводиться на екран „попередній” елемент (a);
- за формулою обчислюється „наступний” елемент, і його значення присвоюється тій же самій змінній (для приклада
a:=a+5);
- останній виток циклу для i=n+1, тому що на кожному витку ми виводимо на екран „попередній” елемент та обчислюємо „наступний”. Тобто при
i=2 виводимо на екран a1, а обчислюємо a2, при i=3 виводимо на екран
a2, а обчислюємо a3 і т.д. Тобто, останній елемент
an виведеться на екран при i=n+1.
|
Приклад 1
Дано натуральне число n . Надрукувати n чисел ai=5i
, i=1, 2, …, n.
Дано: кількість чисел
Знайти: Надрукувати самі числа
У самій формулі для обчислення елементів послідовності не видно, що кожний елемент обчислюється через попередній. Але це можна легко з’ясувати:
a1=51=5
a2=52=25=5*5=a1*5
a3=53=125=25*5=a2*5
a4=54=625=125*5=a3*5
...
Тобто, a1=5, ai=ai-1*5, i=2,3,…,n
.
Результат роботи програми
| Ввід | Вивід | Пояснення |
|---|
| 4 | 5 25 125 625 | Вводимо 4 - кількість чисел. Отримаємо чотири числа, що є степенями 5.
|
Змінні:
Вхідні:
Вихідні:
Проміжні:
Алгоритм
- Спочатку вводимо n – кількість чисел, що потрібно обчислити та вивести на екран.
- До початку циклу присвоїмо початкове значення змінній
a. Воно повинно співпадати з першим числом послідовності a:=5.
- У циклі for i:=2 to n+1 do у операторних дужках будемо виконувати такі дії:
- Оператор write(a,' ') виводить на екран «попереднє» число.
- Оператор a:=a*5 обчислює „наступне” число.
Програма
var i,n:integer;a:longint;
begin
read(n); a:=5;
for i:=2 to n+1 do
Begin
write(a,' '); a:=a*5;
end;
end.
|
Приклад 2
Дано натуральне число n. Надрукувати
n чисел 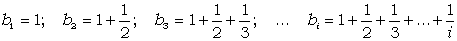 для i=1, 2, …n.
для i=1, 2, …n.
Дано: кількість чисел
Знайти: Надрукувати самі числа
У самій формулі для обчислення елементів послідовності не видно, що кожний елемент обчислюється через попередній. Але це можна легко з’ясувати:
Для обчислення i-го „наступного” числа до попереднього числа додають дріб, у чисельнику якого 1, а у знаменнику порядковий номер „наступного” числа.
Тобто, b1=1; 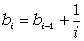 , i=2,3,…n.
, i=2,3,…n.
Результат роботи програми
| Ввід | Вивід | Пояснення |
|---|
| 4 | 1.00 1.50 1.83 2.08 | Вводимо 4 - кількість чисел. Отримаємо чотири дійсних числа що є елементами послідовності
|
Змінні:
Вхідні:
Вихідні:
Проміжні:
Алгоритм
- Спочатку вводимо n – кількість чисел, що потрібно обчислити та вивести на екран.
- До початку циклу присвоїмо початкове значення змінній b. Воно повинно співпадати з першим числом послідовності
b:=1.
- У циклі for i:=2 to n+1 do у операторних дужках будемо виконувати такі дії:
- Оператор write(b:1:2,' ') виводить на екран
"попереднє" число з двома знаками після крапки.
- Оператор b:=b+1/i обчислює "наступне" число.
Програма
var i,n:integer; b:real;
begin
read(n); b:=1;
for i:=2 to n+1 do
begin
write(b:1:2,' ');b:=b+1/i;
end;
end.
|
Приклад 3
Дано натуральне число n. Надрукувати
n чисел, що створюють послідовність Фібоначчі: 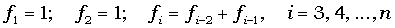
Дано: кількість чисел
Знайти: Надрукувати самі числа
У цій формулі для обчислення елементів послідовності видно, що кожний елемент, починаючи з третього, обчислюється через два попередніх (fi-1 та
fi-2 ).
Правило обчислення елементів послідовності
через два попередніх
- Для значень елементів послідовності потрібно три змінних (a1, a2, a3).
- Перед циклом потрібно:
- присвоїти початкові значення першим двом змінним (a1, a2). Вони повинні співпадати з двома першими елементами послідовності.
- Вивести на екран значення першої змінної (a1).
- У циклі for i:=2 to n do (цикл від 2, бо одне число вже вивели на екран):
- Вивести на екран значення другої змінної (a2).
- За формулою обчислити значення третьої змінної
a3, через a1 та a2.
- Перед переходом на наступний виток циклу переприсвоюємо значення двох „попередніх” елементів:
a1:=a2, a2:=a3.
- Останній виток циклу для i=n, тому що на кожному витку ми виводимо на екран і-й елемент послідовності та обчислюємо
і+1-й елемент. Тобто при i=2 виводимо на екран друге число та обчислюємо третє, при
i=3 виводимо на екран третє число, та обчислюємо четверте і т.д. Тобто, останній елемент виведеться на екран при
i=n.
|
Результат роботи програми
| Ввід | Вивід | Пояснення |
|---|
| 6 | 1 1 2 3 5 8 | Вводимо 6 - кількість чисел. Отримаємо шість елементів послідовності Фібоначчи
|
Змінні:
Вхідні:
Вихідні:
-
f1 – „перше попереднє” число (цілого типу, за мовою)
-
f2 – „друге попереднє” число (цілого типу, за мовою)
-
f3 – „наступне число” (цілого типу, за мовою)
Проміжні:
Алгоритм
- Спочатку вводимо n – кількість чисел, що потрібно обчислити та вивести на екран.
- До початку циклу присвоїмо початкові значення двом попереднім елементам: змінним
f1 та f2. Вони співпадають з двома першими числами послідовності та дорівнюють 1.
- Оператор write(f1,' ') виводить на екран
"перше попереднє" число.
- У циклі for i:=2 to n do у операторних дужках будемо виконувати такі дії:
- Оператор write(f2,' ') виводить на екран
"друге попереднє" число.
- Оператор f3:=f1+f2 обчислює "наступне" число.
- Перед переходом на наступний виток циклу, "друге попереднє" число повинно стати
"першим попереднім" f1:=f2, а "наступне" число повинно стати "другим попереднім"
f2:=f3.
Програма
var i,n:integer; f1,f2,f3:integer;
begin
read(n);
f1:=1; f2:=1; write(f1,' ');
for i:=2 to n do
begin
write(f2,' ');
f3:=f1+f2;
f1:=f2; f2:=f3;
end;
end.
|
Варіанти задач
- Надрукуйте у рядок 10 чисел, якщо перше число 1, а кожне наступне число є добутком попереднього та 0.5.
- Нехай перший член послідовності чисел a=1, а кожний наступний елемент дорівнює сумі попереднього та числа 1.5. Складіть програму обчислення перших 10 елементів цій послідовності.
- Нехай перший член послідовності чисел a=10, а кожний наступний елемент дорівнює добутку попереднього та числа 2.5. Складіть програму обчислення перших 10 елементів цій послідовності.
- Дано натуральні числа N та K. Надрукувати N чисел
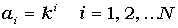 .
.
- Дано натуральне n. Надрукувати n чисел a1=1, ai=2*ai-1+1
, де i=2,3...n
- Складіть програму обчислення перших 10 членів послідовності, якщо i-ий член послідовності має вигляд :xi=2i+3, де i=1,2,...10.
- Дано натуральне n. Надрукувати n чисел ai=i! де i=1, 2, ...n.
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
- Дано натуральне n. Надрукувати n чисел
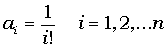 .
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
.
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
- Послідовність чисел a1, a2, a3, ... утворюється за законом:
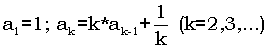 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
- Послідовність чисел a1, a2, a3, ... утворюється за законом:
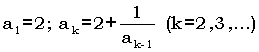 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
- Послідовність чисел a1, a2, a3, ... утворюється за законом:
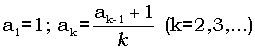 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
- Послідовність чисел a1, a2, a3, ... утворюється за законом:
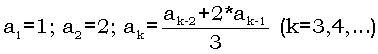 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
- Дано натуральне n. Надрукувати N чисел x1=0.3; x2=-0.3; xi=i+sin(xi-2), де i=3, 4, ..., n.
- Дано натуральне n. Надрукуйте послідовність чисел b1, b2, ... bn, де при i=1, 2, ...n значення bi=2i+3i+1.
Наприклад: b1=2+32; b2=22+33; b3=23+34; ...
- Дано натуральне n. Надрукувати n чисел
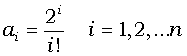 .
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
.
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
- Послідовність u1, u2, u3, ... утворюється за законом u1=0; u2=1; ui=ui-2+ui-1+fi-2 (i=3,4, ...), де fi-2
- відповідний член послідовності Фібоначчі. Дано натуральне число n. Надрукуйте послідовність u1, u2, u3,..., un .
Назад
Зміст
Вперед
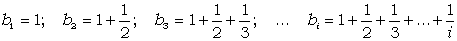 для i=1, 2, …n.
для i=1, 2, …n.
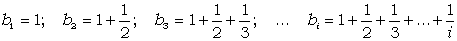 для i=1, 2, …n.
для i=1, 2, …n.
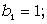
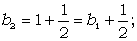
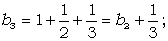
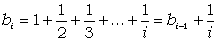
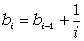 , i=2,3,…n.
, i=2,3,…n.
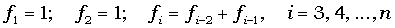
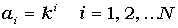 .
.
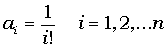 .
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
.
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
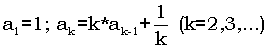 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
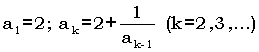 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
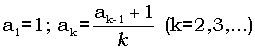 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
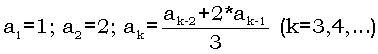 . Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
. Дано натуральне число n. Надрукуйте послідовність чисел a1, a2, a3,..., an .
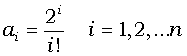 .
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.
.
Пояснення: i факторіал - це добуток чисел від 1 до
i: i!=1*2*3*...*i.