Задачі з вкладеними циклами

Будь-який складний алгоритм завжди складається з декількох простих алгоритмів. Потрібно навчитись їх бачити та комбінувати.

Приклад 1

Знайти 10 перших простих чисел.

В цій задачі використовуються такі алгоритми:

Пошук декількох чисел (10), що задовольняють деякій умові (в нашій задачі: чи є число простим?);
Визначення, чи є число простим?

Зрозуміло, що другий алгоритм вкладений у першій.

Змінні:

Вхідних даних немає.

Вихідні:

n – шукані числа (цілого типу)

Проміжні:

k – лічильник шуканих чисел (цілого типу)
p – ознака наявності дільників (логічного типу, p=false - немає дільників, p=true - є дільники)
i – дільники та параметр циклу (цілого типу)

Алгоритм

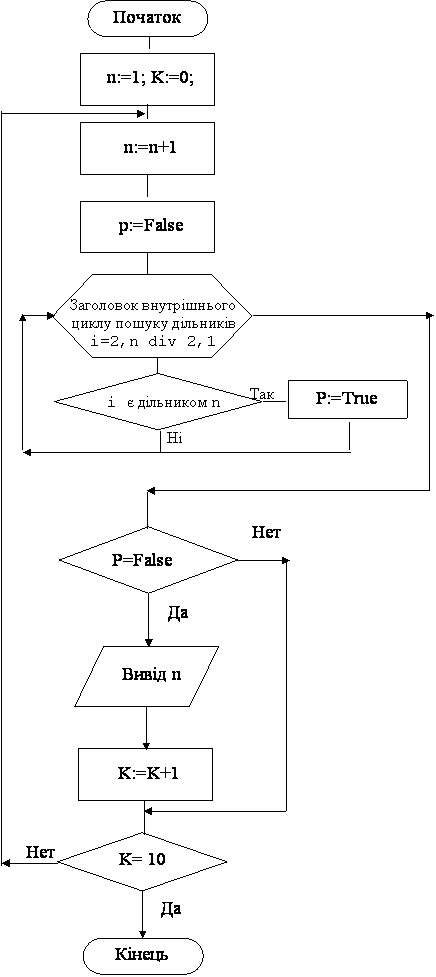
Якщо згадати перший алгоритм, то у ньому:
- до циклу присвоюються початкові значення числу n та кількості чисел k;
- у тілі циклу repeat:
  - збільшується значення числа n;
  - число n перевіряється на якусь умову: якщо умова вірна, то число друкується та збільшується лічильник таких чисел k.
- перевіряється умова завершення циклу: чи надрукована потрібна кількість таких чисел?
  - Якщо так, то цикл завершується і кінець програми.
  - Якщо ні, то перехід на початок тіла циклу.
Зрозуміло, що цей алгоритм буде зовнішнім циклом у нашій програмі, і перебір та перевірку чисел потрібно починати з числа 1.
Умова, на яку у цьому циклі перевіряється число n, – чи є це число простим? Алгоритм, який це визначає, буде вкладений в перший.
Згадаємо, що число n називається простим, якщо в нього немає дільників в інтервалі [2, n div 2].
Тепер згадаємо другий алгоритм, який перевіряє, чи просте число n:
- До циклу присвоюємо початкове значення ознаці p:=false. Тобто вважаємо, що дільників у числа n немає.
- У циклі for i:=2 to n div 2 do будемо шукати дільники числа n. Для кожного будемо перевіряти умову n mod i=0 і, якщо вона вірна (тобто i є дільником n), то встановимо значення ознаки p:=true.
- Коли цикл закінчиться, то перевіримо значення ознаки:
  - якщо p=false, то дільників немає, число n - просте.
  - якщо p=true, то є дільники, число - не просте.
Другий алгоритм вкладений у перший перед перевіркою числа n (виділено жирним).

Блок–схема програми

Програма

Var n,k,i:word; p:boolean;
Begin
n:=1; k:=0;
repeat
   n:=n+1;
   p:=false;
   for i:=2 to n div 2 do
      if n mod i=0 then p:=true;
   if not p then
    begin
      write(n,' '); k:=k+1;
    end;
until k=10;
end.

Результат роботи програми

Відповідь
2 3 5 7 11 13 17 19 23 29

Приклад 2

Дано натуральне число n. Знайдіть його цифровий корінь (від слова цифра, не плутати з коренем квадратним!)

Визначення

Цифровий корінь числа n - це цифра (1, 2, 3,...9), яка обчислюється з цифр числа n за таким алгоритмом:

Знайдемо у числі n суму цифр s.
Перевіримо цю суму s:
- Якщо вона є цифрою (1, 2, 3,...9), то ця сума є цифровий корінь числа n
- Якщо вона не є цифрою (>9), то візьмемо замість числа n отриману суму цифр s та повторимо алгоритм з пункту 1.

Результат роботи програми

Ввід	Вивід
3456	9
555	6

Змінні:

Вхідні:

n – натуральне число (цілого типу)

Вихідні:

сn – цифровий корінь числа n (цілого типу)

Проміжні:

c – остання цифра числа n (цілого типу)
s – сума цифр числа n (цілого типу)

Алгоритм

В цій задачі використовуються такі алгоритми:
- знаходження суми цифр числа;
- заміна числа сумою його цифр, поки ця сума >9.
Зрозуміло, що першій алгоритм вкладений у другий.
Згадаємо алгоритм знаходження суми цифр числа n: обчислюємо останню цифру числа, додаємо її до суми і відкидаємо останню цифру від числа. Все це робимо, поки не переберемо всі цифри числа (у програмі виділено жирним).
У другому алгоритмі:
- Після знаходження суми цифр числа, замінимо число сумою його цифр (n:=s).
- Перевіримо цю суму s:
  - Якщо вона є цифрою (s<=9), то цикл завершується. Виконується перехід на перший оператор після циклу (пункт 5).
  - Якщо вона не є цифрою (s>9), повторимо алгоритм з пункту 3.
Значення отриманої суми присвоюється змінній cn та виводиться на екран.

Програма

var n:longint; c,s,cn:byte;
begin
read(n);
repeat
   s:=0;
   repeat
      c:= n mod 10;
      s:=s+c;
      n:=n div 10;
   until n=0;
   n:=s;
until s<=9;
cn:=s;
writeln(cn);
end.

Приклад 3

Знайдіть цифрові корені всіх простих чисел з інтервалу [100, 200]. Надрукувати число та відповідний цифровий корінь.

Результат роботи програми

Відповідь
101 2 103 4 107 8 109 1 113 5 127 1 131 5 137 2 139 4 149 5 151 7 157 4 163 1 167 5 173 2 179 8 181 1 191 2 193 4 197 8 199 1

Змінні:

Вхідних даних немає.

Вихідні:

n – просте число (цілого типу)
сn – цифровий корінь числа n (цілого типу)

Проміжні:

i – дільники числа n та параметр циклу (цілого типу)
p – ознака простого числа (логічного типу, p=false - просте, p=true - ні)
m – копія числа n (цілого типу)
c – остання цифра числа n (цілого типу)
s – сума цифр числа n (цілого типу)

Алгоритм

В цій задачі використовуються такі алгоритми:
- перебір всіх чисел з інтервалу [100, 200];
- для кожного з цих чисел визначення, чи є воно простим;
- знаходження цифрового кореню кожного простого числа. Цей алгоритм в свою чергу складається з двох алгоритмів (дивись приклад 2).
Зрозуміло, що першій алгоритм - це зовнішній цикл for з параметром n. Він перебирає числа в інтервалі [100, 200].
Другий алгоритм - це пошук дільників i для кожного числа n. Це теж цикл for з параметром i (у програмі виділено жирним). Цей цикл вкладений у перший.
Якщо число просте, тобто дільників у числі немає (p=false), то виконується третій алгоритм, обчислення цифрового кореню числа n (у програмі виділено жирним). Цей алгоритм змінює число n, яке є параметром циклу і не може змінюватись, тому робимо копію цього числа у змінній m та застосовуємо цей алгоритм для змінної m.

Програма

var n,m,i:longint; c,s,cn:byte; p:boolean;
begin
for n:=100 to 200 do
begin
   p:=false;
   for i:=2 to n div 2 do
      if n mod i=0 then p:=true;
   if p=false then
      begin
         m:=n;
         repeat
            s:=0;
            repeat
               c:= m mod 10;
               s:=s+c;
               m:=m div 10;
            until m=0;
            m:=s;
         until s<=9;
         cn:=s;
         write(n,' ',cn,' ');
       end;
end;
end.

Приклад 4

Дано натуральне число n. З’ясуйте, чи є воно симетричним (3434, 345345).

Визначення

Натуральне число n називається симетричним, якщо існує таке натуральне число m, що виконується рівність n div 10^m=n mod 10^m. Число m дорівнює кількості цифр у числі n, поділеній на 2.

Результат роботи програми

Ввід	Вивід
345345	yes
345	no

Змінні:

Вхідні:

n – натуральне число (цілого типу)

Вихідні:

m – степінь числа 10, половина від k кількості цифр числа (цілого типу)

Проміжні:

i – параметр циклу (цілого типу)
k – кількість цифр числа n (цілого типу)
x – копія числа n (цілого типу)
d – 10^m (цілого типу).

Алгоритм

У цій задачі використовуються такі алгоритми:
- знаходження кількості цифр числа;
- піднесення числа до натурального степеня.
Зрозуміло, що алгоритми використовуються послідовно.
Алгоритм програми докладніше:
Вводимо число n.
Запам’ятовуємо це число у змінну x, бо алгоритм знаходження кількості цифр у числі змінює число n.
Встановимо початкове значення k лічильника цифр у числі.
Використаємо алгоритм знаходження кількості цифр числа x: відкидаємо останню цифру від числа, накопичуючи лічильник k. Все це робимо поки не переберемо всі цифри числа (у програмі виділено жирним).
Знайдемо m:=k div 2.
Знайдемо d=10^m (у програмі виділено жирним). Для цього:
- встановимо початкове значення добутку d:=1;
- у циклі for m раз виконаємо оператор d:=d*10.
Порівняємо частку та остачу від ділення n на d:
- Якщо співпадають, то виводимо „число симетричне”;
- Якщо не співпадають, то виводимо „число не симетричне”.

Програма

var n,x,d,i,k,m:longint;
begin
read(n); x:=n;
k:=0;
repeat
    k:=k+1;
    x:=x div 10;
until x=0;
m:=k div 2;
d:=1;
for i:=1 to m do d:=d*10;
   if n div d=n mod d then
        writeln('симетричне ')
   else writeln('несиметричне ');
end.

Приклад 5

Надрукувати перші 5 шестизначних симетричних чисел.

В цій задачі використовуються такі алгоритми:

Пошук декількох чисел (5), що задовольняють деякій умові (в нашій задачі: чи є число симетричним?);
Визначення, чи є число симетричним?

Зрозуміло, що другий алгоритм вкладений у першій.

Змінні:

Вхідних даних немає.

Вихідні:

n – шукані числа (цілого типу)

Проміжні:

t – лічильник шуканих чисел (цілого типу)
x – копія числа n (цілого типу)
i – параметр циклу (цілого типу)
k – кількість цифр числа n (цілого типу)
m – степінь числа 10, половина від k кількості цифр числа (цілого типу)
d – 10^m (цілого типу).

Алгоритм

Якщо згадати перший алгоритм, то у ньому:
- До циклу задаються початкові значення числу n та кількості чисел t .
- В тілі циклу repeat:
  - Збільшується значення числа n;
  - Число n перевіряється на якусь умову: якщо умова вірна, то число друкується та збільшується лічильник таких чисел t.
- Перевіряється умова завершення циклу: чи надрукована потрібна кількість таких чисел?
  - Якщо так, то цикл завершується і кінець програми;
  - Якщо ні, то перехід на початок тіла циклу.
Зрозуміло, що цей алгоритм буде зовнішнім циклом у нашій програмі і перебір та перевірку чисел потрібно починати з числа 100000, бо нам потрібні шестизначні числа.
Умова, на яку у цьому циклі перевіряється число n, це – чи є це число симетричним? Алгоритм, який це визначає буде вкладений в перший.
Тепер згадаємо другий алгоритм, який перевіряє, чи є число n симетричним:
- Обчислюємо k кількість цифр у числі;
- Обчислюємо m половину кількості цифр у числі;
- Обчислюємо d =10^m.
- Перевіряємо рівність n div d=n mod d:
  - Якщо рівність вірна, то число n - симетричне, ми його друкуємо та збільшуємо лічильник таких чисел.
  - Якщо рівність не вірна, то число n - несиметричне.
Другий алгоритм вкладений у перший перед перевіркою числа n (виділено жирним).

Програма

var n,t,k,x,m,d,i:longint;
begin
n:=100000;t:=0;
repeat
   n:=n+1;
   k:=0; x:=n;
   repeat
     k:=k+1;
     x:=x div 10;
   until x=0;
   m:=k div 2;
   d:=1;
   for i:=1 to m do d:=d*10;
     if n div d=n mod d then
       begin
         write(n,’ ‘); t:=t+1;
       end;
until t=5;
end.

Результат роботи програми

Відповідь
100100 101101 102102 103103 104104

Варіанти задач

Надрукувати всі числа з інтервалу [100, 200], цифровий корінь яких кратний 3 (3, 6, 9).
Дано число a. Зайдіть a перших простих чисел.
Дано число a. Знайти просте число, що більше a.
Дано число a. Знайдіть 5 простих чисел, більших a.
Дано число a. Знайти найближче до нього просте число.
Знайдіть всі числа з інтервалу (100, 200), цифровий корінь яких є простим числом (1, 2, 3, 5, 7).
Знайдіть всі числа з інтервалу (100, 200), які кратні своєму цифровому кореню.
Знайдіть цифрові корені чисел Фібоначчі, що належать інтервалу (100, 1000).
Обчисліть та надрукувати цифрові корені досконалих чисел, що належать діапазону (1; 10000). Натуральне число називається досконалим, якщо воно дорівнює сумі своїх дільників, із урахуванням 1 і за винятком самого числа. Наприклад, число 6 - досконале (6=1+2+3).
Знайдіть всі симетричні числа з інтервалу [10000, 1000000].
Знайдіть всі симетричні паліндроми з інтервалу [1000000, 1000000000]. Пояснення: паліндром - це число, яке читається однаково справа наліво та зліва направо, тобто саме число дорівнює перевернутому числу.
Надрукувати з чисел Фібоначчі в інтервалі від 1 до 100, тільки прості числа, а також їх порядкові номери в ряду Фібоначчі.
Для всіх чисел, що належать діапазону [100; 120] обчислити та надрукувати ті дільники, що є членами послідовності Фібоначчі.
Надрукувати всі чотирьохзначні симетричні числа та знайдіти їх кількість.
Знайдіть цифрові корені всіх симетричних чисел, що належать інтервалу (10000, 100000).
Надрукувати перші 10 п’ятизначних паліндромів, що є простими числами. Пояснення: паліндром - це число, яке читається однаково справа наліво та зліва направо, тобто саме число дорівнює перевернутому числу.

Назад Зміст Вперед