Задачі на знаходження дільників

натуральних чисел

Число i є дільником натурального числа n, якщо n mod i=0.

У кожного натурального числа n обов’язково є два дільники: 1 та n.

Всі інші дільники натурального числа n (якщо вини є), знаходяться в інтервалі [2, n div 2].

Натуральне число називається простим, якщо у нього немає дільників в інтервалі [2, n div 2].

Щоб знайти всі дільники числа n, потрібно перевірити всі числа i з інтервалу [1, n] на умову n mod i=0. Тобто це буде такий цикл:

for i:=1 to n do if n mod i=0 then...

Щоб перевірити, чи є число n простим, достатньо перевірити на цю умову всі числа з інтервалу [2, n div 2]. Тобто це буде такий цикл:

for i:=2 to n div 2 do if n mod i=0 then...

Приклад 1

Дано натуральне число n. Знайти всі його дільники, їх кількість та суму.

Дано: натуральне число n.

Знайти: Надрукувати його дільники, підрахувати їх кількість та знайти їх суму.

Результати роботи програми

Ввід	Відповідь	Пояснення
12	1 2 3 4 6 12 6 28	Вводимо число 12. Його дільники: 1 2 3 4 6 12. Кількість дільників –6. Сума дільників – 28.

Змінні:

Вхідні:

n – натуральне число (цілого типу word, бо число натуральне)

Вихідні:

i – дільники та параметр циклу (цілого типу word)
k – кількість дільників (цілого типу word)
s – сума дільників (цілого типу word).

Алгоритм

Спочатку вводимо натуральне число n.
Ми будемо знаходити кількість та суму. Тому присвоїмо початкове значення 0 змінним k та s.
Нам потрібно знайти всі дільники числа n. Вони знаходяться в інтервалі [1, n].
У циклі for i:=1 to n do будемо знаходити ці дільники. Для кожного i будемо перевіряти умову n mod i=0 і, якщо вона вірна (тобто i є дільником n), то
- виводимо на екран цей дільник оператором write(i,' ');
- підраховуємо цей дільник оператором k:=k+1;
- накопичуємо цей дільник у суму оператором s:=s+i.
Коли цикл закінчиться, виводимо знайдені значення кількості та суми на екран оператором writeln(k,' ',s).

Програма

var n,k,s,i:word;
begin
read(n);
k:=0;s:=0;
for i:=1 to n do
    if n mod i=0 then
      begin
         write(i,' '); k:=k+1; s:=s+i;
      end;
writeln(k,' ',s);
end.

Приклад 2

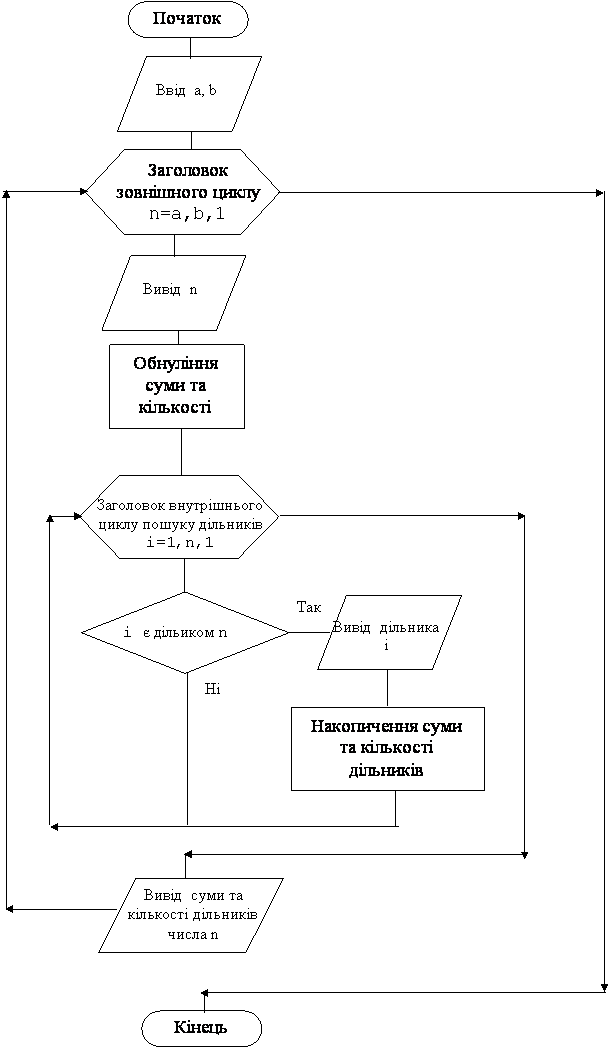
Для кожного натурального числа з інтервалу [A, B] знайдіть всі дільники, їх кількість та суму.

Дано: два натуральних числа A та B.

Знайти: Для кожного з чисел A, A+1, A+2,..., B знайти всі дільники, підрахувати їх кількість та знайти їх суму.

Результати роботи програми

Ввід	Відповідь	Пояснення
a=10 b=14	дільники числа 10: 1 2 5 10 k=4 s=18 дільники числа 11: 1 11 k=2 s=12 дільники числа 12: 1 2 3 4 6 12 k=6 s=28 дільники числа 13: 1 13 k=2 s=14 дільники числа 14: 1 2 7 14 k=4 s=24	Вводимо числа 10 та 14. Для кожного з чисел 10, 11, 12, 13, 14, знаходимо дільники, їх кількість та суму. Перед дільниками виводимо на екран і само число

Змінні:

Вхідні:

A – ліва границя інтервалу (цілого типу word, бо числа натуральні)
B – права границя інтервалу (цілого типу word, бо числа натуральні)

Вихідні:

n – натуральне число з інтервалу [A, B] та параметр зовнішнього циклу (цілого типу word, бо число натуральне)
i – дільники числа n та параметр внутрішнього циклу (цілого типу word)
k – кількість дільників числа n (цілого типу word)
s – сума дільників числа n (цілого типу word).

Алгоритм

Спочатку вводимо натуральні числа A та B, що є границями інтервалу.
Для кожного числа n із цього інтервалу ми повинні повністю виконати попередній алгоритм, починаючи з пункту 2. Тому у нас будуть вкладені цикли:
- зовнішній цикл: for n:=a to b do
  - перебирає числа n з інтервалу [A, B];
  - виводить ці числа на екран write(n);
  - для кожного числа n встановлює початкове значення для кількості та суми дільників s:=0; k:=0. Це обов’язково потрібно зробити у зовнішньому циклі, але перед внутрішнім.
- внутрішній цикл for i:=1 to n do if n mod i=0 then для кожного числа n знаходить дільники та:
  - виводить на екран цей дільник оператором write(i,' ');
  - підраховує цей дільник оператором k:=k+1;
  - накопичує цей дільник у суму оператором s:=s+i.
- Коли внутрішній цикл закінчиться, виводимо знайдені значення кількості та суми для даного числа n на екран оператором writeln(k,' ',s) та переходимо на наступний виток зовнішнього циклу для обробки наступного числа.

Блок–схема програми

Програма

var a,b,n,i,k,s:word;
begin
write(a=');read(a);
write('b=');read(b);
for n:=a to b do
begin
   write(дільники числа ',n,': ');
   s:=0;k:=0;
   for i:=1 to n do
      if n mod i=0 then
        begin
          write(i,' ');
          k:=k+1; s:=s+i;
        end;
   writeln(' k=',k,' s=',s);
end;
end.

Приклад 3

Для кожного з чисел з інтервалу від 300 до 400 знайти суму дільників. Вивести на екран числа, у яких сума дільників кратна 10, а також саму суму дільників.

Знайти: Для кожного з чисел 300, 301, 302, ..., 400 додати всі дільники, і, якщо сума буде кратна 10, то вивести на екран число та знайдену суму.

Результати роботи програми

Відповідь	Пояснення
n=304 s=620 n=312 s=840 n=316 s=560 n=319 s=360 n=323 s=360 n=327 s=440 n=328 s=630 n=342 s=780 n=343 s=400 n=344 s=660 n=348 s=840 n=349 s=350 n=351 s=560 n=354 s=720 n=356 s=630 n=358 s=540 n=359 s=360 n=360 s=1170 n=376 s=720 n=377 s=420 n=378 s=960 n=379 s=380 n=380 s=840 n=384 s=1020 n=389 s=390 n=395 s=480 n=398 s=600 n=399 s=640	В програму нічого не вводиться. Числа у відповіді мають коментарі: спочатку виводиться число n, а потім сума його дільників s.

Змінні:

Вхідних даних немає

Вихідні:

n – натуральне число з інтервалу [300,400] та параметр зовнішнього циклу (цілого типу word, бо число натуральне)
i – дільники числа n та параметр внутрішнього циклу (цілого типу word)
s – сума дільників числа n (цілого типу word).

Алгоритм

Так же як і у попередньому прикладі, у нас будуть вкладені цикли:
- зовнішній цикл: for n:=300 to 400 do
  - перебирає числа n з інтервалу [300,400];
  - для кожного числа n встановлює початкове значення для суми дільників s:=0;
  - внутрішній цикл for i:=1 to n do if n mod i=0 then для кожного числа n знаходить суму дільників s:=s+i.
- Коли внутрішній цикл закінчиться, перевіряємо знайдену суму s і, якщо вона кратна 10 (s mod 10=0), то виводимо на екран число n та знайдену суму оператором write('n=',n,'s=',s) та переходимо на наступний виток зовнішнього циклу для обробки наступного числа.

Програма

var n,i,s:word;
begin
for n:=300 to 400 do
begin
   s:=0;
   for i:=1 to n do
     if n mod i=0 then s:=s+i;
   if s mod 10=0 then
   write(' n=',n,' s=',s);
end;
end.

Приклад 4

Дано натуральне число n. Визначити, чи є воно простим?

Дано: натуральне число n.

Знайти: З’ясувати, чи є у числа дільники у інтервалі [2, n div 2].

Результати роботи програми

Ввід	Відповідь	Пояснення
12	No	У числа 12 в інтервалі [2,6] є дільники: 2, 3, 4, 6. Тому число не є простим.
17	Yes	У числа 17 в інтервалі [2,8] немає дільників. Тому число є простим.

Змінні:

Вхідні:

n – натуральне число (цілого типу word, бо число натуральне)

Вихідні:

p – ознака наявності дільників (логічного типу, p=false немає дільників, p=true є дільники )

Проміжні:

i – дільники та параметр циклу (цілого типу word)

Алгоритм

Спочатку вводимо натуральне число n.
Ми будемо використовувати алгоритм з ознакою. Тому присвоїмо початкове значення ознаці p:=false. Тобто вважаємо, що дільників немає.
Тепер у циклі for i:=2 to n div 2 do будемо шукати дільники. Для кожного i будемо перевіряти умову n mod i=0 і, якщо вона вірна (тобто i є дільником n), то установимо значення ознаки p:=true.
Коли цикл закінчиться, то перевіримо значення ознаки:
- Якщо p=false, то дільників немає, число просте, відповідь 'yes'.
- Якщо p=true, то є дільники, число не просте, відповідь 'no'.

Програма

var n,i: word; P:boolean;
begin
read(n);p:=false;
for i:=2 to n div 2 do
if n mod i=0 then p:=true;
if not p then writeln('yes')
else writeln('no');
end.

Приклад 5

Знайдіть в інтервалі [A, B] всі прості числа.

Дано: два натуральних числа A та B.

Знайти: Для кожного з чисел A, A+1, A+2,..., B з’ясувати, чи є воно простим. Якщо число просте, то вивести його на екран.

Результати роботи програми

Ввід	Відповідь	Пояснення
10 14	11 13	Вводимо числа 10 та 14. Для кожного з чисел 10, 11, 12, 13, 14, шукаємо дільники в інтервалі [2,n div 2]. У числа 10 в інтервалі [2,5] є дільники 2 та 5, тобто число не просте. У числа 11 в інтервалі [2,5] немає дільників, тобто число просте і тому виводиться на екран. У числа 12 в інтервалі [2,6] є дільники 2, 3, 4 та 6, тобто число не просте. У числа 13 в інтервалі [2,6] немає дільників, тобто число просте і тому виводиться на екран. У числа 14 в інтервалі [2,7] є дільники 2 та 7, тобто число не просте.

Змінні:

Вхідні:

A – ліва границя інтервалу (цілого типу word, бо числа натуральні)
B – права границя інтервалу (цілого типу word, бо числа натуральні)

Вихідні:

p – ознака наявності дільників (логічного типу, p=false немає дільників, p=true є дільники )

Проміжні:

n – натуральне число з інтервалу [A, B] та параметр зовнішнього циклу (цілого типу word, бо число натуральне)
i – дільники числа n та параметр внутрішнього циклу (цілого типу word)

Алгоритм

Спочатку вводимо натуральні числа A та B, що є границями інтервалу.
Для кожного числа n із цього інтервалу ми повинні повністю виконати попередній алгоритм, починаючи з пункту 2. Тому у нас будуть вкладені цикли:
- зовнішній цикл: for n:=a to b do
  - перебирає числа n з інтервалу [A, B]
  - присвоює початкове значення ознаці p:=false. Тобто вважаємо, що дільників у числа n немає. Це обов’язково потрібно зробити у зовнішньому циклі, але перед внутрішнім.
- У внутрішньому циклі for i:=2 to n div 2 do будемо шукати дільники числа n. Для кожного i будемо перевіряти умову n mod i=0 і, якщо вона вірна (тобто i є дільником n), то установимо значення ознаки p:=true.
- Коли внутрішній цикл закінчиться, то перевіримо значення ознаки:
  - якщо p=false, то дільників немає, число n просте і тому виводиться на екран оператором write(n,' '), а потім виконується перехід на наступний виток зовнішнього циклу для обробки наступного числа.
  - якщо p=true, то є дільники, число не просте, число не виводиться, виконується перехід на наступний виток зовнішнього циклу для обробки наступного числа.

Програма

var n,i,a,b: word; P:boolean;
begin
read(a,b);
for n:=a to b do
begin
   p:=false;
   for i:=2 to n div 2 do
     if n mod i=0 then p:=true;
   if not p then write(n,' ');
end;
end.

Варіанти задач

Дано натуральне число n. Вивести на екран всі його парні дільники.
Дано натуральне число n. Знайти суму його непарних дільників.
Дано натуральне число n. Знайти кількість його парних дільників.
Для кожного цілого числа з інтервалу [10,15] знайдіть всі непарні дільники.
Дано натуральне число n. Надрукуйте його дільники та знайдіть середнє арифметичне його парних дільників.
Знайдіть всі прості трьохзначні числа.
Надрукуйте всі трьохзначні паліндроми, що є простими числами.
В інтервалі [A, B] знайдіть кількість простих чисел.
Для кожного цілого числа з інтервалу [30, 36] знайдіть кількість його парних дільників.
Для кожного цілого числа з інтервалу [15, 20] знайдіть суму його непарних дільників.
Знайдіть суму непарних дільників для кожного з цілих чисел від 50 до 70.
Для кожного цілого числа з інтервалу [16, 24] знайдіть середнє арифметичне його парних дільників.
Для кожного цілого числа з інтервалу [120; 140] знайдіть всі непарні дільники та їх кількість.
Для кожного цілого числа з інтервалу [A, B] знайдіть кількість його парних дільників.
Для кожного цілого числа з інтервалу [A, B] знайдіть всі його дільники, що кратні 3.
З інтервалу [15, 25] виведіть на екран числа, у яких 4 дільники.

Назад Зміст Вперед